Ultimate Periodicity And Dfas
Ultimate Periodicity and DFAs: Ultimate periodicity is a property that captures a central property of regular sets (recall the definition of ultimate periodicity given in Definition 5.1, page 76).
Theorem . If L is a regular language over an alphabet Σ, then the set Len = {length(w) | w ∈ L} is ultimately periodic.
Note: The converse is not true. For example, the language {0n1n | n ≥ 0} has strings whose lengths are ultimately periodic, and yet this language is not regular.
A good way to see that Theorem 10.3 is true is as follows. Given any DFA D over some alphabet Σ, consider the NFA N obtained from D by first replacing every transition labeled by a symbol in Σ \ {a} by a. In other words, we are applying a homomorphism that replaces every symbol of the DFA by a. Hence, the resulting machine is bound to be an NFA, and the lengths of strings in its language will be the same as those of the strings in the language of the original DFA (in other words, what we have described is a length-preserving homomorphism). Now, if we convert this NFA to a DFA, we will get a machine that starts out in a start state and proceeds for some number (≥ 0) of steps before it “coils” into itself. In other words, it attains a lasso shape. It cannot have any other shape than the ‘coil’ (why?).
This coiled DFA shows that the length of strings in the language of any DFA is ultimately periodic with the period defined by the size of the coil. We now take an extended example to illustrate these ideas. Consider the DFA built over Σ = {a, b, c, d, f} using the following command pipeline:
echo ’(ad)* ((abc)((acf)* (da)*)d)’ | retofm | fmdeterm | fmmin | grail2ps.perl - | gv -
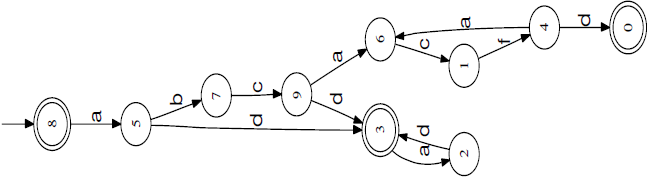
The DFA generated by converting every symbol to a and determinizing the result is as follows.
echo ’(aa)* ((aaa)((aaa)* (aa)*)a)’ | retofm | fmdeterm | fmmin | grail2ps.perl - | gv -

The length of strings in the language of this DFA is ultimately periodic, with the values of the constants n = 2 and p = 6 as per the definition of UP appearing in Section 5.2.1.