Unrestricted Grammar

UNRESTRICTED GRAMMAR: The grammars in the Chomsky hierarchy allows productions of the form

a->b

where a and b are arbitrary strings of grammar symbols, with a ≠ λ.

These types of grammars as called “Unrestricted grammars”. The 4-tuple notation G = (V,T, P, S ) is used for unrestricted grammars also.

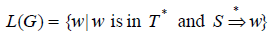
=>* denotes the reflexive and transitive closure of the relation Þ.

THE O REM (I): If L is L(G) for unrestricted grammar G = (V,T, P, S ) , then L is an r.e. language.

THE O REM (II): If L is an r.e. language, then L = L(G) for some unrestricted grammar G.

RANDOM-ACCESS MACHINE: A randon access machine is defined as follows:

Data Types: The only data type supported is the Natural Numbers 0, 1, 2, 3,......... But the numbers may be very large.

Variables: An orbitrary number of variables are allowed. Each variable is capable of holding a single natural number. All variables are initialized to 0.

Tests: The only test allowed is <variable> = 0.

Statements:There are the following types of statements in the language:

(a)    if <test> then <statement> else <statement>;

(b)    while <test> do <statements>;

(c)    <variable> : = <variable> 1; (increment)

(d)    <variable>: = <variable> –1; (decrement)

It is to be noted that decrementing a variable whose value is already zero has no effect.

Statements to be executed in sequence (<statement>; <statement>; <statement>; ...... are allowed and parentheses are used to group a sequence of statement into a single statement. This language is very equivalent in power to a Turing machine. This can be proved by using the language to implement a Turing machine, and then using a Turing machine to emulate the language. This language is so powerful to compute anything that can be computed in any programming language.