Validity Of First-order Logic Is Undecidable

Validity of first-order logic is undecidable: Valid formulas are those that are true under all interpretations. For example,
∀x.f (x) = g(x) ⇒ ∃a.f (a) = g(a).
Validity stems from the innate structure of the formula, as it must remain true under every conceivable interpretation. We will now summarize Floyd’s proof that the validity problem for firstorder logic is undecidable. First, an abbreviation: for σi ∈ {0, 1}, use the abbreviation
fσ1,σ2,...,σn(a) = fσn(fσn−1 (. . . fσ1(a)) . . .).
The proof proceeds by building a FOL formula for a given “Post system” (an instance of Post’s correspondence problem). Given a Post system S = {(α1, β1), (α2, β2), . . . , (αn, βn), n ≥ 1 over Σ = {0, 1}, construct the wff WS (we will refer to the two antecedents of WS as A1 and A2, and its consequent as C1):

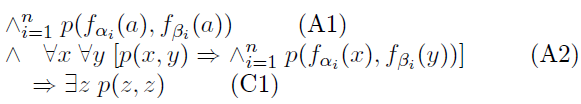
We now prove that S has a solution iff WS is valid.
Part 1. (WS valid) ⇒ (S has a solution). If valid, it is true for all interpretations. Pick the following interpretation:

a = ε
f0(x) = x0 (string ‘x’ and string ‘0’ concatenated)
f1(x) = x1 (similar to the above)
p(x, y) = There exists a non-empty sequence i1i2 . . . im such that
x = αi1αi2 . . .αim and y = βi1βi2 . . .βim
Under this interpretation, parts A1 and A2 of WS are true. Here is why:

Under the above interpretation, fαi(a) = εαi = αi and similarly fβi(a) = βi.
Thus A1 becomes ∧ni=1 p(αi, βi). Each conjunct in this formula is true by p’s interpretation; hence A1 is true.
The part [p(x, y) ⇒ ∧ni=1 p(fαi(x), fβi(y))] reduces to the following claim: p(x, y) is true means that x and y can be written in the form x = αi1αi2 . . .αim and y = βi1βi2 . . .βim; the consequent of this implication then says that we can append some αi and the corresponding βi to x and y, respectively. The consequent is also true by p’s interpretation. Thus A2 is also true.
Since WS is valid (true), C1 must also be true. C1 asserts that the Post system S has a solution, namely some string z that lends itself to being interpreted as some sequence αi1αi2 . . .αim as well as βi1βi2 . . .βim. That is, αi1αi2 . . .αim = z = βi1βi2 . . .βim.

Part 2. (WS valid) ⇐ (S has a solution).
If S has a solution, let it be the sequence i1i2 . . . im. In other words, αi1αi2 . . .αim = βi1βi2 . . . βim = Soln. Now, in order to show that WS is valid, we must show that for every interpretation it is true. We approach this goal by showing that under every interpretation where the antecedents ofWS, namely A1 and A2, are true, the consequent, namely C1, is also true (if any antecedent is false, WS is true, so this case is not considered).
From A1, we conclude that
p(fαi1 (a), fβi1 (a))
is true. Now using A2 as a rule of inference, we can conclude through Modus ponens, that
p(fαi2 (fαi1 (a)), fβi2 (fβi1 (a))
is true. In other words,
p(fαi1αi2 (a), fβi1βi2 (a))
is true. We continue this way, applying the functions in the order dictated by the assumed solution for S; in other words, we arrive at the assertion that the following is true (notice that the subscripts of f describe the order in which the solution to S considers the α’s and β’s):
p(fαi1αi2 ...αim(a), fβi1βi2...βim(a)).

However, since
αi1αi2 . . .αim = βi1βi2 . . .βim = Soln,
we have essentially shown that
p(fSoln(a), fSoln(a)).
Now, p(fSoln(a), fSoln(a)) means that there exists a z such that p(z, z), namely z = fSoln(a).

Valid FOL formulas are enumerable
It was proved by G¨odel in his dissertation that first-order predicate calculus is complete. In other words, there are axiomatizations of firstorder logic in which every valid formula has a proof. Hence, by enumerating proofs, one can enumerate all valid first-order logic formulas. Thus the set of valid FOL formulas is recursively enumerable (or is Turing recognizable).