Concept of Phasor: A phase vector ("phasor") is a representation of a sine wavewhose amplitude (A), phase (θ), and frequency (ω) are time-invariant. It is a subset of a more general concept called analytic representation. Phasors reduce the dependencies on these parameters to three independent factors, thereby simplifying certain kinds of calculations. In particular the frequency factor, which also includes the time-dependence of the sine wave, is often common to all the components of a linear combination of sine waves. Using phasors, it can be factored out, leaving just the static amplitude and phase information to be combined algebraically (rather than trigonometrically). Similarly, linear differential equationscan be reduced to algebraicones. The term phasor therefore often refers to just those two factors. In older texts, a phasor is also referred to as a sinor.

Addition of two out-of-phase sinusoidal signals is rather complicated in the time domain. An example could be the sum of voltages across a series connection of a resistor and an inductor. Phasors simplify this analysis by considering only the amplitude and phase components of the sine wave. Moreover, they can be solved using complex algebra or treated vectorially using a vector diagram.

Consider a vector quantity A in the complex plane as shown in Figure (a). Then

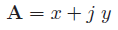                       .........................................eq. (1)

where x = Acos θ and y = Asin θ, therefore

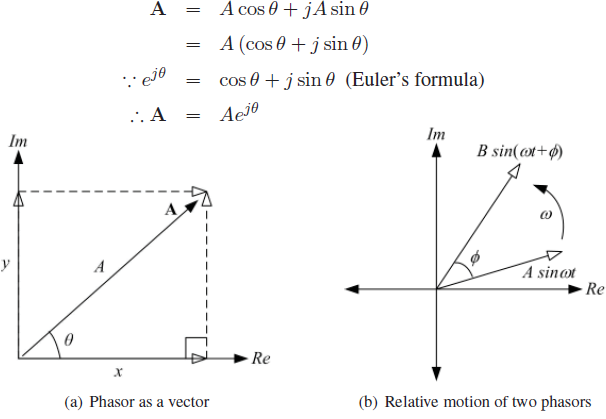Vector representation of a phasor.

Equation A =Ae^jθ  is the phasor notation of the vector A where A is the length of the vector or amplitude of the signal and θ is the angle which A makes with a reference phasor.

Rotating Vector Concept Let θ = ωt, therefore A = Aejωt where ω is the angular velocity and t is the time. Then A can be regarded as a vector rotating with an angular velocity ω. Now if two phasors are rotating with the same velocity as illustrated in Figure (b), then their relative positions are unchanged with respect to time and therefore can be added.

Two or more sinusoidal signals can be added mathematically using phasors if they all have the same angular velocities.

Polar form is also commonly used to represent a phasor and is given by the magnitude (modulus) and phase (argument) of the signal i.e.,

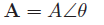
It may be convenient to transform the polar form into cartesian form (Equation 1) and vice versa when adding two sinusoidal signals.