Conductors And Insulators

Conductors and Insulators: Materials through which charge flows readily are called conductors. Examples include most metals, such as silver, gold, copper, and aluminum. Copper is used extensively for the conductive paths on electric circuit boards and for the fabrication of electrical wires.

Insulators are materials that do not allow charge to move easily. Examples include glass, plastic, ceramics, and rubber. Electric current cannot be made to flow through an insulator, since a charge has great difficulty moving through it. One sees insulating (or dielectric) materials often wrapped around the center conducting core of a wire.

one can say qualitatively that a conductor has a very low resistance to the flow of charge, whereas an insulator has a very high resistance to the flow of charge. Charge-conducting abilities of various materials vary in a wide range. Semiconductors fall in the middle between conductors and insulators, and have a moderate resistance to the flow of charge. Examples include silicon, germanium, and gallium arsenide.

Current and Magnetic Force: The rate of movement of net positive charge per unit of time through a cross section of a conductor is known as current,

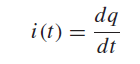
The SI unit of current is the ampere (A), which represents 1 coulomb per second.The net charge transferred at a particular time is the net area under the current–time curve from the beginning of time to the present,

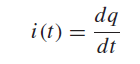
While Coulomb’s law has to do with the electric force associated with two charged bodies, Ampere’s law of force is concerned with magnetic forces associated with two loops of wire carrying currents by virtue of the motion of charges in the loops. Note that isolated current elements do not exist without sources and sinks of charges at their ends; Considering a differential element d .l1 of loop 1 and a differential element d .l2 of loop 2, the differential magnetic forces d . F21 and d . F12 experienced by the differential current elements I1 d .l1, and I2 d .l2, due to I2 and I1, respectively, are given by

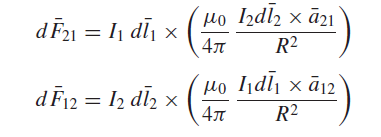
where .a21 and .a12 are unit vectors along the line joining the two current elements, R is the distance between the centers of the elements, μ0 is the permeability of free space with units of N/A2 or commonly known as henrys per meter (H/m).

1. The magnitude of the force is proportional to the product of the two currents and the product of the lengths of the two current elements.

2. The magnitude of the force is inversely proportional to the square of the distance between the current elements.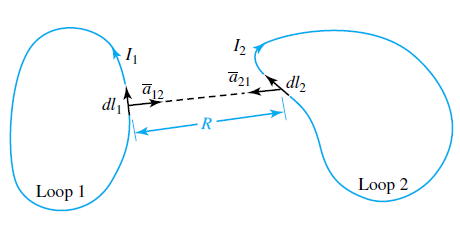

Illustration of Coulomb’s law.

3. To determine the direction of, say, the force acting on the current element I1 d ¯l1, the cross product d ¯l2 × ¯a21 must be found. Then crossing d ¯l1 with the resulting vector will yield the direction of d ¯ F21.
4. Each current element is acted upon by a magnetic field due to the other current element,

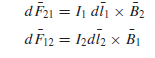
where B is known as the magnetic flux density vector with units of N/A · m, commonly known as webers per square meter (Wb/m2) or tesla (T).