Distinction Between Line And Phase Voltages, And Line And Phase Currents
Distinction between line and phase voltages, and line and phase currents: The voltage produced by a single winding of a three-phase circuit is called the line-to-neutral voltage, or simply the phase voltage, Ephase In a wye-connected three-phase ac power source, the phase voltage is measured between the neutral line and any one of points A, B, and C. This results in the following three distinct phase voltages: EA-N, EB-N, and EC-N.
The voltage between any two windings of a three-phase circuit is called the lineto line voltage, or simply the line voltage Eline. In a wye-connected three-phase ac power source, the line voltage is √3 (approximately 1.73) times greater than the phase voltage (i.e., Eline = √3 Ephase). In a delta-connected three-phase ac power source, the voltage between any two windings is the same as the voltage across the third winding of the source (i.e.,Eline = Ephase), as shows Figure 3b. In both cases, this results in the following three distinct line voltages: EA-B, EB-C, and EC-A.
The three line wires (wires connected to points A, B, and C) and the neutral wire of a three-phase power system are usually available for connection to the load, which can be connected in either a wye configuration or a delta configuration. The two types of circuit connections are illustrated in Figure 1. Circuit analysis demonstrates that the voltage (line voltage) between any two line wires, or lines, in a wye-connected load is √3 times greater than the voltage (phase voltage) across each load resistor. Furthermore, the line current line flowing in each line of the power source is equal to the phase current Iphase flowing in each load resistor. On the other hand, in a delta-connected load, the voltage (phase voltage) across each load resistor is equal to the line voltage of the source. Also, the line current is √3 times greater than the current (phase current) in each load resistor. The phase current in a delta connected load is therefore √3 times smaller than the line current.
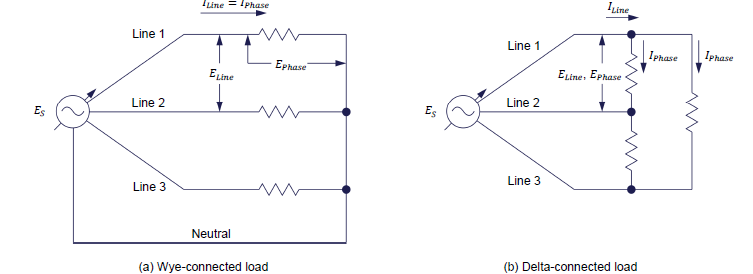
Figure 1. Types of load connections.
The relationships between the line and phase voltages and the line and phase currents simplify the analysis of balanced three-phase circuits. A shorthand way of writing these relationships is given below.
