Efficiency Of Transformer

Efficiency of transformer: In a practical transformer we have seen mainly two types of major losses namely core and copper losses occur. These losses are wasted as heat and temperature of the transformer rises. Therefore output power of the transformer will be always less than the input power drawn by the primary from the source and efficiency is defined as

We have seen that from no load to the full load condition the core loss, Pcore remains practically constant since the level of flux remains practically same. On the other hand we know that the winding currents depend upon the degree of loading and copper loss directly depends upon the square of the current and not a constant from no load to full load condition. We shall write a general expression for efficiency for the transformer operating at x per unit loading and delivering power to a known power factor load. Let,

KVA rating of the transformer be = S
Per unit degree of loading be = x
Transformer is delivering = x S KVA
Power factor of the load be = cos θ
Output power in KW = xS cos θ
Let copper loss at full load (i.e., x = 1) = P_cu
Therefore copper loss at x per unit loading = x2 P_cu
Constant core loss = P_{core .......................1}

Therefore efficiency of the transformer for general loading will become:

.............................2

If the power factor of the load (i.e., cos θ) is kept constant and degree of loading of the transformer is varied we get the efficiency Vs degree of loading curve as shown in the figure 1. For a given load power factor, transformer can operate at maximum efficiency at some unique value of loading i.e., x. To find out the condition for maximum efficiency, the above equation for η can be differentiated with respect to x and the result is set to 0. Alternatively, the right hand side of the above equation can be simplified to, by dividing the numerator and the denominator by x. the expression for η then becomes:

For efficiency to be maximum,d/dx(Denominator) is set to zero and we get,

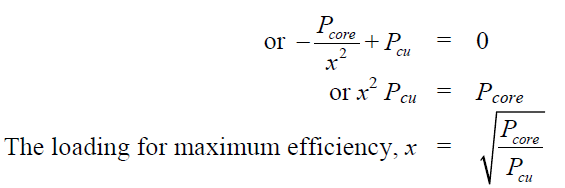
efficiency VS degree of loading curves fig 1