Hysteresis Loss & Loop Area

Hysteresis loss & loop area: In other words the operating point trace the perimeter of the closed area QFMNKPRTSEQ. This area is called the B-H loop of the material. We will now show that the area enclosed by the loop is the hysteresis loss per unit volume per cycle variation of the current. In the interval    0≤ωt ≤π/2 i is ve and di/dt is also ve, moving the operating point from M to P along the path MNKP. Energy absorbed during this interval is given by the shaded area MNKPLTM shown in fig.(A) (i).

In the interval π/2≤ωt≤π, is ve but di/dt is –ve, moving the operating point from P to T along the path PRT. Energy returned during this interval is given by the shaded area PLTRP shown in fig.(A) (ii). Thus during the ve half cycle of current variation net amount of energy absorbed is given by the shaded area MNKPRTM which is nothing but half the area of the loop.
In the interval π≤ωt≤3π/2 , i is –ve and di/dt is also –ve, moving the operating point from T to Q along the path TSEQ. Energy absorbed during this interval is given by the shaded area QJMTSEQ shown in fig.(A) (iii).

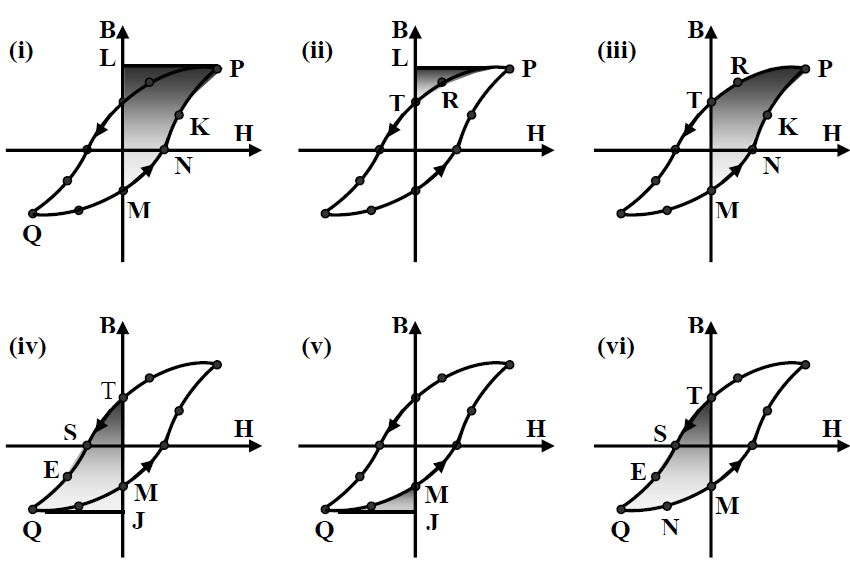
fig.(A) B-H loop with sinusoidal current.

In the interval 3π/2<ωt<2π,  i is –ve but di/dt is ve, moving the operating point from Q to M along the path QEM. Energy returned during this interval is given by the shaded area QJMFQ shown in fig.(A) (iv).
Thus during the –ve half cycle of current variation net amount of energy absorbed is given by the shaded area QFMTSEQ which is nothing but the other half the loop area.

Therefore total area enclosed by the B-H loop is the measure of the hysteresis loss per unit volume per unit cycle. To reduce hysteresis loss one has to use a core material for which area enclosed will be as small as possible.