Introduction of Eddy Current & Hysteresis Losses: we assumed the exciting current to be constant d.c. We also came to know how to calculate flux (φ) or flux density (B) in the core for a constant exciting current. When the exciting current is a function of time, it is expected that flux (φ) or flux density (B) will be functions of time too, since φ produced depends on i. In addition if the current is also alternating in nature then both the magnitude of the flux and its direction will change in time. The magnetic material is now therefore subjected to a time varying field instead of steady constant field with d.c excitation. Let:

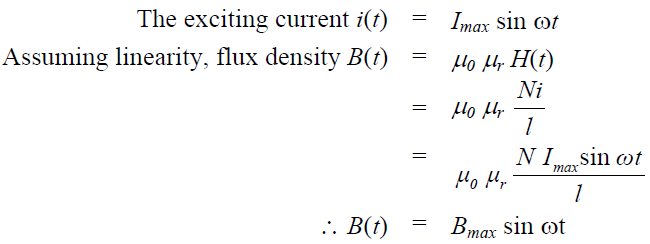
Voltage induced in a stationary coil placed in a time varying field: If normal to the area of a coil, a time varying field φ(t) exists as in figure (A), then an emf is induced in the coil. This emf will appear across the free ends 1 & 2 of the coil. Whenever we talk about some voltage or emf, two things are important, namely the magnitude of the voltage and its polarity. Faraday’s law tells us about the both. Mathematically it is written as e(t) = -N(dφ/dt)

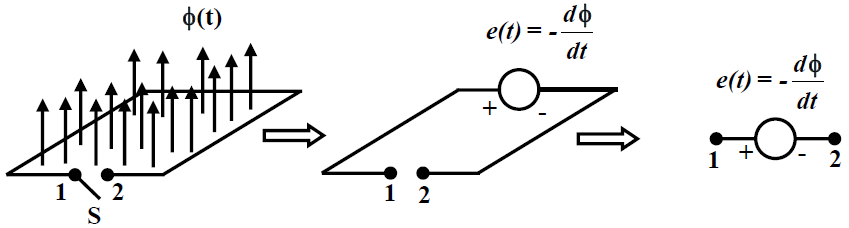FIG.(A)

Let us try to understand the implication of this equation a bit deeply. φ(t) is to be taken normal to the surface of the coil. But a surface has two normals; one in the upward direction and the other in downward direction for the coil shown in the figure. Which one to take? The choice is entirely ours. In this case we have chosen the normal along the upward direction. This direction is obtained if you start your journey from the terminal-2 and reach the terminal-1 in the anticlockwise direction along the contour of the coil. Once the direction of the normal is chosen what we have to do is to express φ(t) along the same direction. Then calculate N(dφ/dt) and put a – ve sign before it. The result obtained will give you e₁₂ i.e., potential of terminal-1 wrt terminal-2. In other words, the whole coil can be considered to be a source of emf wrt terminals 1 & 2 with polarity as indicated. If at any time flux is increasing with time in the upward direction, dφ/dt is ve and e₁₂ will come out to be – ve as well at that time. On the other hand, at any time flux is decreasing with time in the upward direction, dφ/dt is – ve and e₁₂ will come out to be ve as well at that time. Mathematically let:

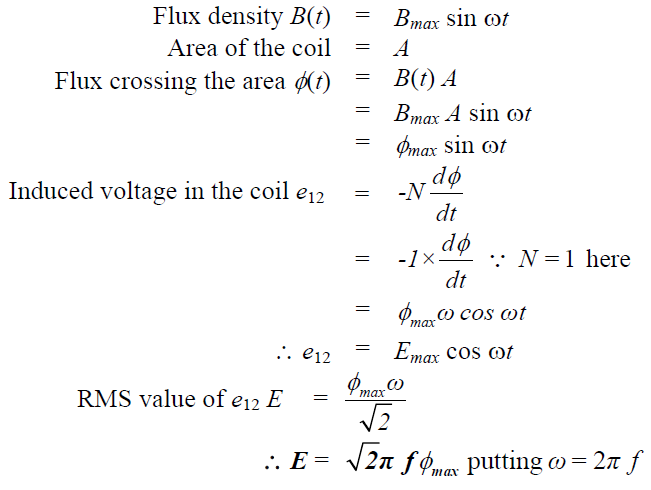
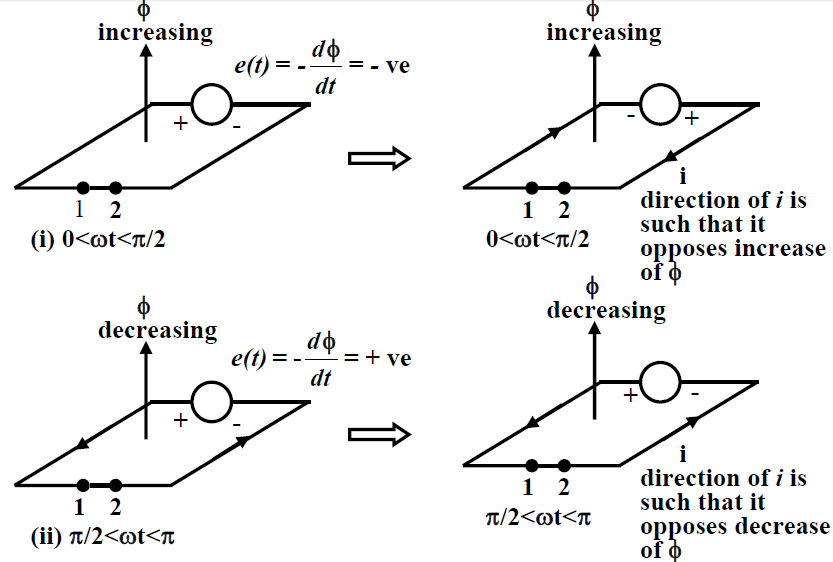If the switch S is closed, this voltage will drive a circulating current ic in the coil the direction of which will be such so as to oppose the cause for which it is due. Correct instantaneous polarity of the induced voltage and the direction of the current in the coil are shown in figure (B), for different time intervals with the switch S closed. In the interval 0<ωt<π/2, dφ/dt is positive

------fig(b) Direction of induced current.