Phase Difference: the Sinusoidal Waveform  (Sine Wave) can be presented graphically in the time domain along an horizontal zero axis, and that sine waves have a positive maximum value at time π/2, a negative maximum value at time 3π/2, with zero values occurring along the baseline at 0, π and 2π. However, not all sinusoidal waveforms will pass exactly through the zero axis point at the same time, but may be "shifted" to the right or to the left of 0^o by some value when compared to another sine wave. For example, comparing a voltage waveform to that of a current waveform. This then produces an angular shift or Phase Difference between the two sinusoidal waveforms. Any sine wave that does not pass through zero at t = 0 has a phase shift.

The phase difference or phase shift as it is also called of a sinusoidal waveform is the angle Φ (Greek letter Phi), in degrees or radians that the waveform has shifted from a certain reference point along the horizontal zero axis. In other words phase shift is the lateral difference between two or more waveforms along a common axis and sinusoidal waveforms of the same frequency can have a phase difference.

The phase difference, Φ of an alternating waveform can vary from between 0 to its maximum time period, T of the waveform during one complete cycle and this can be anywhere along the horizontal axis between, Φ = 0 to 2π (radians) or Φ  = 0 to 360^o depending upon the angular units used. Phase difference can also be expressed as a time shift of τ in seconds representing a fraction of the time period, T for example, 10mS or - 50uS but generally it is more common to express phase difference as an angular measurement.

Then the equation for the instantaneous value of a sinusoidal voltage or current waveform we developed in the previous Sinusoidal Waveform  will need to be modified to take account of the phase angle of the waveform and this new general expression becomes.

Phase Difference Equation:

Where:

•   A_m  -  is the amplitude of the waveform.
•   ωt  -  is the angular frequency of the waveform in radian/sec.
•   Φ (phi)  -  is the phase angle in degrees or radians that the waveform has shifted either left or right from the reference point.

Phase Relationship of a Sinusoidal Waveform:

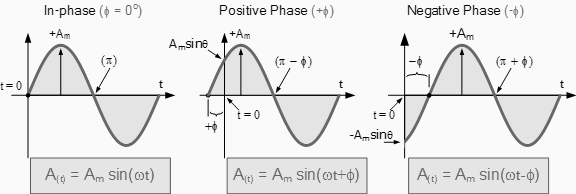
Firstly, lets consider that two alternating quantities such as a voltage, v and a current, i have the same frequency ƒ in Hertz. As the frequency of the two quantities is the same the angular velocity, ω must also be the same. So at any instant in time we can say that the phase of voltage, v will be the same as the phase of the current, i. Then the angle of rotation within a particular time period will always be the same and the phase difference between the two quantities of v and i will therefore be zero and Φ = 0. As the frequency of the voltage, v and the current, i are the same they must both reach their maximum positive, negative and zero values during one complete cycle at the same time (although their amplitudes may be different). Then the two alternating quantities, v and i are said to be "in-phase"