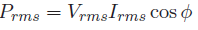Power In Ac Circuits
Power in AC Circuits: From DC circuit analysis, power is given by the following relationship:
P = V I Watts
Therefore the instantaneous power is given by p(t) = v(t) · i(t). Let i(t) = Im sin(ωt β) be the current flowing through an impedance, Z, then the voltage across the impedance will be v(t) = Vm sin(ωt α). Therefore
p(t) = VmIm sin(ωt α) sin(ωt β)
Using the trigonometric identity
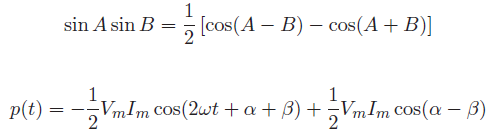
The first term is a time-varying sinusoidal waveform with twice the frequency of v(t) or i(t) and an average value of zero. On the other hand, the second term is a constant quantity and is called the DC level or average value of the power signal, p(t) or average power delivered to the load i.e.,
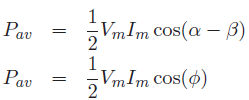eq....................(1)
where φ = α − β is the phase angle between v(t) and i(t).
The waveform p(t) is plotted in Figure (below) for an arbitrary value of φ where the negative shaded portion of the waveform is the power returned (not absorbed by the load) to the source.
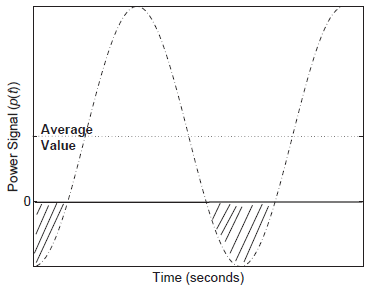Power supplied to a generic load impedance.
For a purely resistive load (φ = 00), Equation(1) becomes
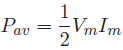
and the resulting power signal, p(t) is depicted in Figure (a). In this case, there is no negative portion of the waveform and hence all the power is dissipated in the load.
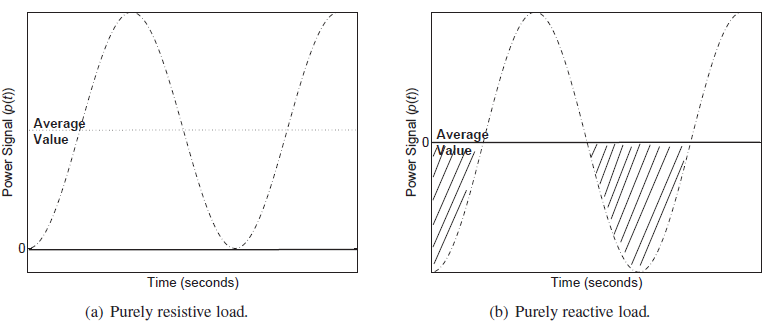For a purely reactive load, i.e., Z = ±jX, φ = 900 and Pav = 0. The power signal waveform is
drawn in Figure (b) showing that the power oscillates between the source and electric/magnetic
field of the load. Thus the power dissipated in the load is zero for a purely reactive load.
In terms of RMS voltage and current, the average power is given by
