Simple Series Resonance

Simple series resonance: A similar effect happens in series inductive/capacitive circuits. When a state of resonance is reached (capacitive and inductive reactances equal), the two impedances cancel each other out and the total impedance drops to zero!

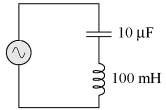
At 159.155 Hz the following values are valid:

Z_L = 0 j100 Ω
Z_C = 0 - j100 Ω
Z_series = Z_C Z_L
Z_series = 0 - j100 Ω 0 j100 Ω = 0 Ω

With the total series impedance equal to 0 Ω at the resonant frequency of 159.155 Hz, the result is a short circuit across the AC power source at resonance. In the circuit drawn above, this would not be good. I'll add a small resistor in series along with the capacitor and the inductor to keep the maximum circuit current somewhat limited.

Review

The total impedance of a series LC circuit approaches zero as the power supply frequency approaches resonance.
The same formula for determining resonant frequency in a simple tank circuit applies to simple series circuits as well.
Extremely high voltages can be formed across the individual components of series LC circuits at resonance, due to high current flows and substantial individual component impedances.