Steinmetz’s Empirical Formula For Hysteresis Loss
Steinmetz’s empirical formula for hysteresis loss: Based on results obtained by experiments with different ferromagnetic materials with sinusoidal currents, Charles Steimetz proposed the empirical formula for calculating hysteresis loss analytically.
Where, the coefficient kh depends on the material and n, known as Steinmetz exponent, may vary from 1.5 to 2.5. For iron it may be taken as 1.6.
Seperation of core loss: The sum of hyteresis and eddy current losses is called core loss as both the losses occur within the core (magnetic material). For a given magnetic circuit with a core of ferromagnetic material, volume and thickness of the plates are constant and the total core loss can be expressed as follows.
It is rather easier to measure the core loss with the help of a wattmeter (W) by energizing the N turn coil from a sinusoidal voltage of known frequency as shown in figure(A).
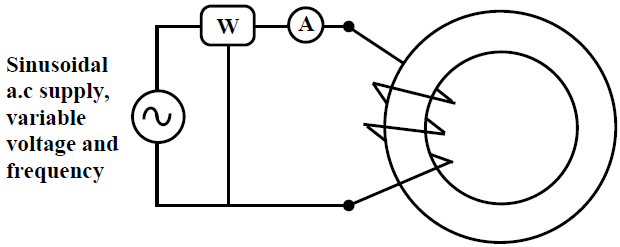fig(A) Core loss measurement
Let A be the cross sectional area of the core and let winding resistance of the coil be negligibly small (which is usually the case), then equating the applied rms voltage to the induced rms voltage of the coil we get:
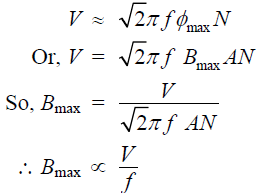
The above result i.e., Bmax ∝ V/f is important because it tells us that to keep Bmax constant at rated value at lower frequency of operation, applied voltage should be proportionately decreased. In fact, from the knowledge of N (number of turns of the coil) and A (cross sectional area of the core), V (supply voltage) and f (supply frequency) one can estimate the maximum value of the flux density from the relation 
. This point has been further discussed in the future lesson on transformers.
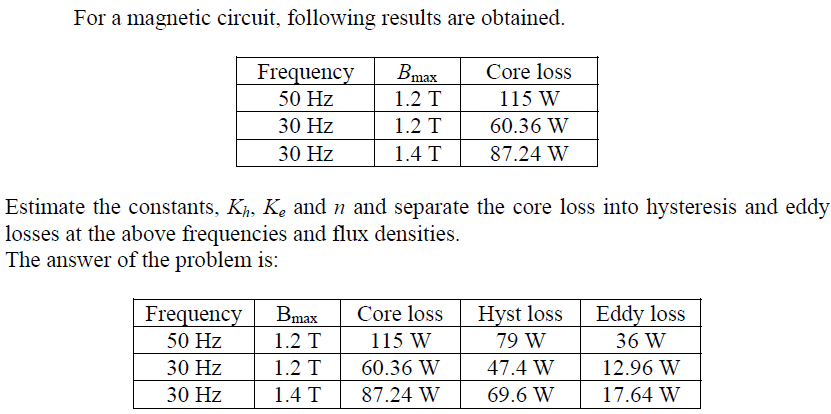
Now coming back to the problem of separation of core loss into its components: we note that there are three unknowns, namely Kh, Ke and n (Steinmetz’s exponent) to be determined in the equation 
of this equation is nothing but the wattmeter reading of the experimental set up shown in Figure A. Therefore, by noting down the wattmeter readings corresponding to three different applied voltages and frequencies, we can have three independent algebraic equations to solve for Kh, Ke and n. However, to simplify the steps in solving of the equations two readings may be taken at same flux density (keeping V/f ratio constant) and the third one at different flux density. To understand this, solve the following problem and verify the answers given.
