The Cosine Waveform: So we now know that if a waveform is "shifted" to the right or left of 0^o when compared to another sine wave the expression for this waveform becomes A_m sin(ωt ± Φ). But if the waveform crosses the horizontal zero axis with a positive going slope 90^o or π/2 radians before the reference waveform, the waveform is called a Cosine Waveform and the expression becomes.

Cosine Expression:

The Cosine Wave, simply called "cos", is as important as the sine wave in electrical engineering. The cosine wave has the same shape as its sine wave counterpart that is it is a sinusoidal function, but is shifted by 90^o or one full quarter of a period ahead of it.

Phase Difference between a Sine wave and a Cosine wave:

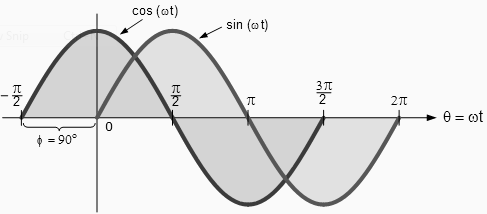
Alternatively, we can also say that a sine wave is a cosine wave that has been shifted in the other direction by -90^o. Either way when dealing with sine waves or cosine waves with an angle the following rules will always apply.

Sine and Cosine Wave Relationships:

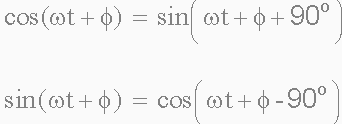
When comparing two sinusoidal waveforms it more common to express their relationship as either a sine or cosine with positive going amplitudes and this is achieved using the following mathematical identities.

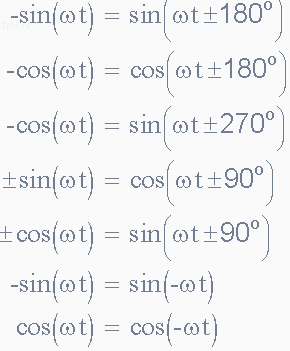
By using these relationships above we can convert any sinusoidal waveform with or without an angular or phase difference from either a sine wave into a cosine wave or vice versa.