Application Of Rouths Stability Criterion To Control System Analysis

Application of Routh's stability criterion to control system analysis

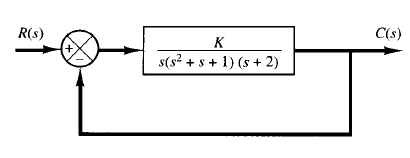
Fig: 1 Control system

Routh's stability criterion is of limited usefulness in linear control system analysis mainly because it does not suggest how to improve relative stability or how to stabilize an unstable system. It is possible, however, to determine the effects of changing one or two parameters of a system by examining the values that cause instability.

In the following, we shall consider the problem of determining the stability range of a parameter value. Consider the system shown in Figure 1. Let us determine the range of K for stability. The closed-loop transfer function is

For stability, K must be positive, and all coefficients in the first column must be positive. Therefore,

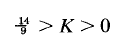
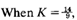the system becomes oscillatory and, mathematically, the oscillation is sustained at constant amplitude.

Relative stability analysis

Routh's stability criterion provides the answer to the question of absolute stability. This, in many practical cases, is not sufficient. We usually require information about the relative stability of the system. A useful approach for examining relative stability is to shift the s-plane axis and apply Routh's stability criterion.

That is, we substitute

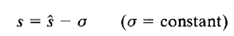
into the characteristic equation of the system, write the polynomial in terms of 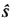; and apply Routh's stability criterion to the new polynomial in .

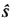The number of changes of sign in the first column of the array developed for the polynomial in 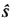is equal to the number of roots that are located to the right of the vertical line s = -σ. Thus, this test reveals the number of roots that lie to the right of the vertical line s = -σ.