Closed-loop Frequency Response For Nonunity-feedback Systems
Closed-loop frequency response for non-unity-feedback systems
The constant M and N loci and the Nichols chart cannot be directly applied to control systems with nonunity feedback, but rather require a slight modification. If the closed-loop system involves a nonunity-feedback transfer function, then the closed-loop transfer function may be written
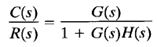
where G(s) is the feedforward transfer function and H(s) is the feedback transfer function. Then C(jω)/R(jω) can be written
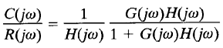
The magnitude and phase angle of
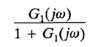
where G1(jω) = G(jω )H(jω), may be obtained easily by plotting the G1(jω) locus on the Nichols chart and reading the values of M and N at various frequency points. The closed loop frequency response C(jω)/R(jω) may then be obtained by multiplying G1(jω)/[1 G1(jω)] by 1/H(jω).
This multiplication can be made without difficulty if we draw Bode diagrams for G1(jω)/[l G1(jω)] and H(jω) and then graphically subtract the magnitude of H(jω) from that of G1(jω)/[1 G1(jω)] and also graphically subtract the phase angle of H(jω) from that of G1(jω)/[1 G l(jω)]. Then the resulting log-magnitude curve and phase-angle curve give the closed-loop frequency response C(jω)/R(jω).
To obtain acceptable values of Mr, ωr, and ωb for |C(jω)/R(jω)|, a trial-and-error process may be necessary. In each trial, the G1(jω) locus is varied in shape. Then Bode diagrams for G1(jω)/[1 G1(jω)] and H(jω) are drawn, and the closed-loop frequency response C(jω )R(jω) is obtained. The values of Mr, ωr, and ωb are checked until they are acceptable.