Closed-loop Frequency Response Of Unity-feedback Systems

Closed-loop frequency response of unity-feedback systems

 

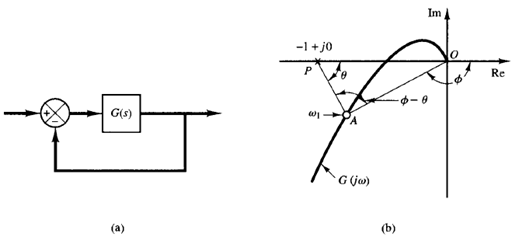
Fig: 1 (a) Unity-feedback system; (b) determination of closed-loop frequency response from open-loop frequency response

 

For a stable closed-loop system, the frequency response can be obtained easily from that of the open loop. Consider the unity-feedback system shown in Figure 1(a). The closed-loop transfer function is

 

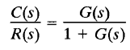
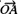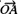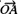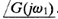In the Nyquist or polar plot shown in Figure 1(b), the vector represents G(jω₁), where ω₁ is the frequency at point A. The length of the vector is |G(jω₁)| and the angle of the vector is . The vector 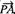, the vector from the -1 j0 point to the Nyquist locus, represents 1 G(jω₁). Therefore, the ratio of 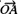to 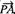represents the closed-loop frequency response, or

 

 

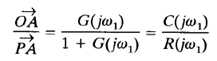
The magnitude of the closed-loop transfer function at ω = ω₁ is the ratio of the magnitudes of 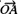to 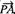. The phase angle of the closed-loop transfer function at ω = ω₁ is the angle formed by the vectors 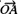to 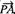, that is Φ - θ, shown in Figure 1(b). By measuring the magnitude and phase angle at different frequency points, the closed-loop frequency-response curve can be obtained.

 

 Let us define the magnitude of the closed-loop frequency response as M and the phase angle as a, or

 

 

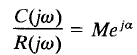
The constant magnitude loci and constant phase-angle loci are convenient in determining the closed-loop frequency response from the polar plot or Nyquist plot.