Closed-loop System Subjected To A Disturbance

Closed-loop system subjected to a disturbance

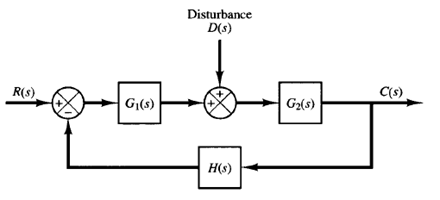
Fig: 1 Closed-loop system subjected to a disturbance.

Figure 1 shows a closed loop system subjected to a disturbance. When two inputs (the reference input and disturbance) are present in a linear system, each input can be treated independently of the other; and the outputs corresponding to each input alone can be added to give the complete output. The way each input is introduced into the system is shown at the summing point by either a plus or minus sign.

Consider the system shown in Figure 1. In examining the effect of the disturbance D(s), we may assume that the system is at rest initially with zero error; we may then calculate the response CD(s) to the disturbance only. This response can be found from

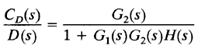
On the other hand, in considering the response to the reference input R(s), we may assume that the disturbance is zero. Then the response CR(S) to the reference input R(s) can be obtained from

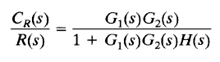
The response to the simultaneous application of the reference input and disturbance can be obtained by adding the two individual responses. In other words, the response C(s) due to the simultaneous application of the reference input R(s) and disturbance D(s) is given by

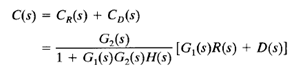
Consider now the case where |G₁(s)H(s)| >> 1 and |G₁(s)G₂(s)H(s)| >> 1. In this case, the closed-loop transfer function C_D(s)/D(s) becomes almost zero, and the effect of the disturbance is suppressed. This is an advantage of the closed-loop system.

On the other hand, the closed-loop transfer function C_R(s)/R(s) approaches 1/H(s) as the gain of G₁(S)G₂(S)H(s) increases. This means that if |G₁(s)G₂(s)H(s)| >> 1 then the closed-loop transfer function C_R(s)/R(s) becomes independent of G₁(s) and G₂(S) and becomes inversely proportional to H(s) so that the variations of G₁(s) and G₂(s) do not affect the closed-loop transfer function C_R(s)/R(s). This is another advantage of the closed-loop system. It can easily be seen that any closed-loop system with unity feedback, H(s) = 1, tends to equalize the input and output.