Comments On Phase And Gain Margins

Comments on phase and gain margins

It is also important to point out that conditionally stable systems will have two or more phase crossover frequencies, and some higher-order systems with complicated numerator dynamics may also have two or more gain crossover frequencies, as shown in Figure 1. For stable systems having two or more gain crossover frequencies, the phase margin is measured at the highest gain crossover frequency.

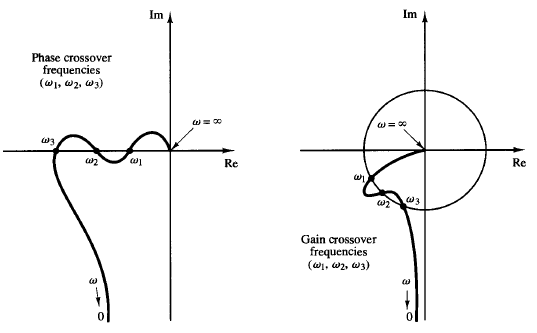
Fig: 1 Polar plots showing more than two phase or gain crossover frequencies

The phase and gain margins of a control system are a measure of the closeness of the polar plot to the -1 j0 point. Therefore, these margins may be used as design criteria. It should be noted that either the gain margin alone or the phase margin alone does not give a sufficient indication of the relative stability. Both should be given in the determination of relative stability.

For a minimum-phase system, both the phase and gain margins must be positive for the system to be stable. Negative margins indicate instability. Proper phase and gain margins ensure us against variations in the system components and are specified for definite values of frequency.

The two values bound the behavior of the closed-loop system near the resonant frequency. For satisfactory performance, the phase margin should be between 30° and 60°, and the gain margin should be greater than 6 dB. With these values, a minimum-phase system has guaranteed stability, even if the open-loop gain and time constants of the components vary to a certain extent. Although the phase and gain margins give only rough estimates of the effective damping ratio of the closed-loop system, they do offer a convenient means for designing control systems or adjusting the gain constants of systems.

For minimum-phase systems, the magnitude and phase characteristics of the open loop transfer function are definitely related. The requirement that the phase margin be between 30° and 60° means that in a Bode diagram the slope of the log-magnitude curve at the gain crossover frequency should be more gradual than -40 dB/ decade.

 In most practical cases, a slope of -20 dB/decade is desirable at the gain crossover frequency for stability. If it is -40 dB/decade, the system could be either stable or unstable. (Even if the system is stable, however, the phase margin is small.) If the slope at the gain crossover frequency is -60 dB/decade or steeper, the system is most likely unstable.