Concept Of Transfer Function

Transfer function:

The transfer function of a linear, time-invariant, differential equation system is defined as the ratio of the Laplace transform of the output (response function) to the Laplace transform of the input (driving function) under the assumption that all initial conditions are zero.

Consider the linear time-invariant system defined by the following differential equation:

 

 

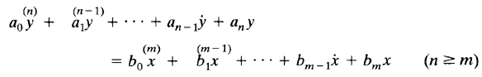
where y is the output of the system and x is the input. The transfer function of this system is obtained by taking the Laplace transforms of both sides of Equation, under the assumption that all initial conditions are zero, or

 

 

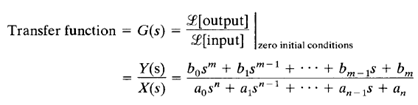
By using the concept of transfer function, it is possible to represent system dynamics by algebraic equations in s. If the highest power of s in the denominator of the transfer function is equal to n, the system is called an nth-order system.

 

Comments on transfer function:

 The applicability of the concept of the transfer function is limited to linear, time-invariant, differential equation systems. The transfer function approach, however, is extensively used in the analysis and design of such systems. In what follows, we shall list important comments concerning the transfer function. (Note that in the list a system referred to is one described by a linear, time invariant, differential equation.)

 

1. The transfer function of a system is a mathematical model in that it is an operational method of expressing the differential equation that relates the output variable to the input variable.

2. The transfer function is a property of a system itself, independent of the magnitude and nature of the input or driving function.

3. The transfer function includes the units necessary to relate the input to the output; however, it does not provide any information concerning the physical structure of the system. (The transfer functions of many physically different systems can be identical.)

4. If the transfer function of a system is known, the output or response can be studied for various forms of inputs with a view toward understanding the nature of the system.

5. If the transfer function of a system is unknown, it may be established experimentally by introducing known inputs and studying the output of the system. Once established, a transfer function gives a full description of the dynamic characteristics of the system, as distinct from its physical description.