Conditionally Stable Systems Of A Polar Plot

Conditionally stable systems of a polar plot

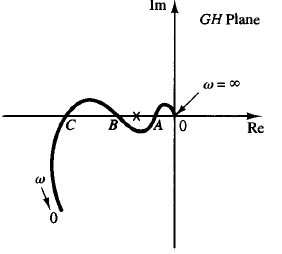
Fig: 1 Polar plot of a conditionally stable system

Figure 1 shows an example of a G(jω)H(jω) locus for which the closed-loop system can be made unstable by varying the open-loop gain. If the open-loop gain is increased sufficiently, the G(jω)H(jω) locus encloses the -1 j0 point twice, and the system becomes unstable.

 If the open-loop gain is decreased sufficiently, again the G(jω)H(jω) locus encloses the -1 j0 point twice. For stable operation of the system considered here, the critical point -1 j0 must not be located in the regions between OA and BC shown in Figure 1.

 Such a system that is stable only for limited ranges of values of the open-loop gain for which the -1 j0 point is completely outside the G(jω)H(jω) locus is a conditionally stable system.

A conditionally stable system is stable for the value of the open-loop gain lying between critical values, but it is unstable if the open-loop gain is either increased or decreased sufficiently. Such a system becomes unstable when large input signals are applied, since a large signal may cause saturation, which in turn reduces the open-loop gain of the system. It is advisable to avoid such a situation.