Conditionally Stable Systems

Conditionally stable systems:

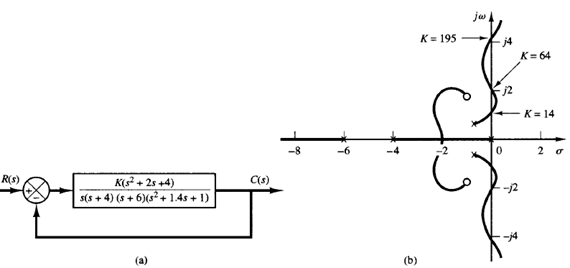
Fig: 1 (a) Conditionally stable system; (b) root-locus plot.

Consider the system shown in Figure 1(a). The root loci for this system can be plotted by applying the general rules and procedure for constructing root loci. A root-locus plot for this system is shown in Figure 1(b).

It can be seen that this system is stable only for limited ranges of the value of K; that is, 0 < K < 14 and 64 < K < 195. The system becomes unstable for 14 < K < 64 and 195 < K. If K assumes a value corresponding to unstable operation, the system may break down or may become nonlinear due to a saturation nonlinearity that may exist. Such a system is called conditionally stable.

In practice, conditionally stable systems are not desirable. Conditional stability is dangerous but does occur in certain systems, in particular, a system that has an unstable feed forward path.

Such a feed forward path may occur if the system has a minor loop. It is advisable to avoid such conditional stability since, if the gain drops beyond the critical value for some reason, the system becomes unstable.

 Note that the addition of a proper compensating network will eliminate conditional stability. An addition of a zero will cause the root loci to bend to the left. Hence conditional stability may be eliminated by adding proper compensation.