Correlation Between Transfer Functions And State-space Equations
Correlation between transfer functions and state-space equations
we will study how to derive the transfer function of a single-input-single output system from the state-space equations.
Let us consider the system whose transfer function is given by
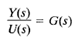
This system may be represented in state space by the following equations:
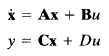
where x is the state vector, u is the input, and y is the output. The Laplace transforms of the above equation are given by
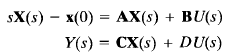
Since the transfer function was previously defined as the ratio of the Laplace transform of the output to the Laplace transform of the input when the initial conditions were zero, we assume that x(o) in the above equation is zero. Then we have
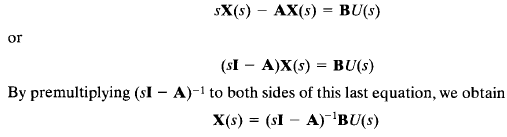
Rearranging we have,
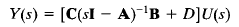
Rearranging again we have,
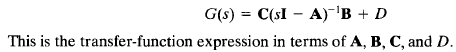
Note that the right-hand side of above equation involves (sI - A)-I. Hence G(s) can be written as
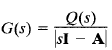
where Q(s) is a polynomial in s. Therefore, |sI – A| is equal to the characteristic polynomial of G(s). In other words, the eigenvalues of A are identical to the poles of G(s).