Cut Off Frequency And Bandwidth
Cutoff frequency and bandwidth
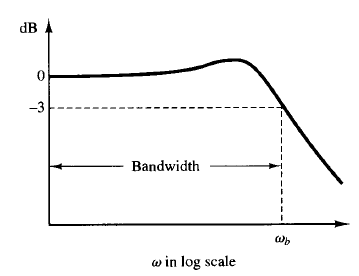
Fig: 1 Plot of a closed-loop frequency response curve showing cutoff frequency ωband bandwidth
Referring to Figure 1, the frequency ωb at which the magnitude of the closed-loop frequency response is 3 dB below its zero frequency value is called the cut off frequency. Thus
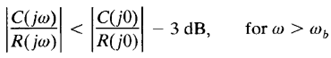
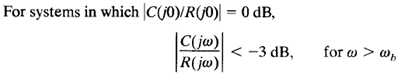
The closed-loop system filters out the signal components whose frequencies are greater than the cutoff frequency and transmits those signal components with frequencies lower than the cutoff frequency.
The frequency range 0 ≤ ω ≤ ωb in which the magnitude of the closed loop does not drop -3 dB is called the bandwidth of the system. The bandwidth indicates the frequency where the gain starts to fall off from its low-frequency value. Thus, the bandwidth indicates how well the system will track an input sinusoid. Note that for a given ωn the rise time increases with increasing damping ratio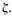 
On the other hand, the bandwidth decreases with the increase of 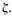Therefore, the rise time and the bandwidth are inversely proportional to each other.
The specification of the bandwidth may be determined by the following factors:
1. The ability to reproduce the input signal. A large bandwidth corresponds to a small rise time, or fast response. Roughly speaking, we can say that the bandwidth is proportional to the speed of response.
2. The necessary filtering characteristics for high-frequency noise. For the system to follow arbitrary inputs accurately, it is necessary that the system have a large bandwidth. From the viewpoint of noise, however, the bandwidth should not be too large. Thus, there are conflicting requirements on the bandwidth, and a compromise is usually necessary for good design. Note that a system with large bandwidth requires high-performance components. So the cost of components usually increases with the bandwidth.
Cut off rate:
The cutoff rate is the slope of the log-magnitude curve near the cutoff frequency. The cutoff rate indicates the ability of a system to distinguish the signal from noise.
It is noted that a closed-loop frequency response curve with a steep cutoff characteristic may have a large resonant peak magnitude, which implies that the system has relatively small stability margin.