Differential Equations Of Physical Systems

DIFFERENTIAL EQUATIONS OF PHYSICAL SYSTEMS

The differential equations describing the dynamic performance of a physical system are obtained by utilizing the physical laws of the process. This approach applies equally well to mechanical, electrical, fluid, and thermodynamic systems. Consider the torsional spring-mass system in Figure 1 with applied torque T_a(t). Assume the torsional spring element is massless. Suppose we want to measure the torque T_s(t) transmitted to the mass m. Since the spring is massless, the sum of the torques acting on the spring itself must be zero, or

which implies that T_s(t) = T_a(t). We see immediately that the external torque T_a(t) applied at the end of the spring is transmitted through the torsional spring. Because of this, we refer to the torque as a through-variable. In a similar manner, the angular rate difference associated with the torsional spring element is

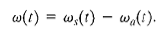
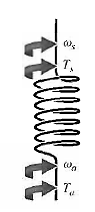
Fig: 1

Thus, the angular rate difference is measured across the torsional spring element and is referred to as an across-variable. These same types of arguments can be made for most common physical variables (such as force, current, volume, flow rate, etc.).

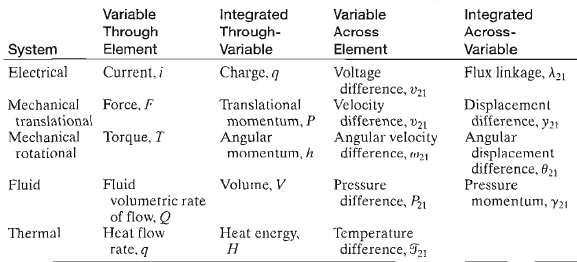
Table 1:  Summary of Through- and Across-Variables for Physical Systems