First-order Factors In Bode Diagrams

First-order factors in Bode diagrams

The log magnitude of the first-order factor 1/(1 jωT) is

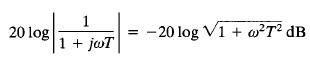
For low frequencies, such that ω << 1/T, the log magnitude may be approximated by

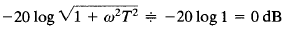
Thus, the log-magnitude curve at low frequencies is the constant O-dB line. For high frequencies, such that ω >> 1/T,

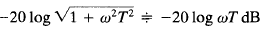
This is an approximate expression for the high-frequency range. At ω = 1/T, the log magnitude equals 0 dB; at ω = 10/T, the log magnitude is -20 dB. Thus, the value of -20 log ωT dB decreases by 20 dB for every decade of ω. For ω >>1/T, the log-magnitude curve is thus a straight line with a slope of -20 dB/decade (or -6 dB/octave).

Our analysis show that the logarithmic representation of the frequency-response curve of the factor 1/(1 jw1) can be approximated by two straight-line asymptotes, one a straight line at 0 dB for the frequency range 0 < ω < 1/T and the other a straight line with slope -20 dB/decade (or -6 dB/octave) for the frequency range 1/T < ω < ∞.

The exact log-magnitude curve, the asymptotes, and the exact phase-angle curve are shown in Figure 1.

The frequency at which the two asymptotes meet is called the corner frequency or break frequency. For the factor 1/(1 jωT), the frequency w = 1/T is the corner frequency since at ω = 1/T the two asymptotes have the same value. (The low-frequency asymptotic expression at ω = 1/T is 20 log 1 dB = 0 dB, and the high-frequency asymptotic expression at ω = 1/Tis also 20 log 1 dB = 0 dB.) The corner frequency divides the frequency-response curve into two regions, a curve for the low-frequency region and a curve for the high-frequency region. The corner frequency is very important in sketching logarithmic frequency-response curves. The exact phase angle Φ of the factor 1/(1 jω T) is

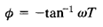
At zero frequency, the phase angle is 0°. At the corner frequency, the phase angle is

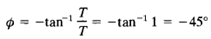
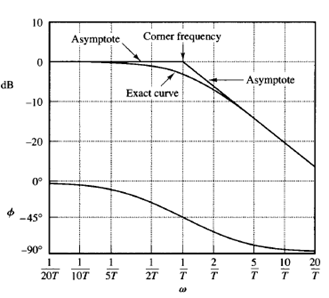
Fig: 1 Log-magnitude curve together with the asymptotes and phase angle curve

At infinity, the phase angle becomes -90°. Since the phase angle is given by an inverse-tangent function, the phase angle is skew symmetric about the inflection point at Φ = -45°.