General Rules For Constructing Roots Loci

General rules for constructing root loci

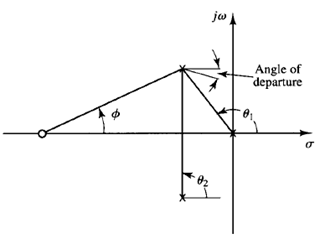
Fig: 2 Construction of the root locus

The angle of departure is shown in Figure 2.

6. Find the points where the root loci may cross the imaginary axis. The points where the root loci intersect the jω axis can be found easily by (a) use of Routh's stability criterion or (b) letting s = jω in the characteristic equation, equating both the real part and the imaginary part to zero, and solving for wand K. The values of w thus found give the frequencies at which root loci cross the imaginary axis. The K value corresponding to each crossing frequency gives the gain at the crossing point.

7. Taking a series of test points in the broad neighborhood of the origin of the s plane, sketch the root loci. Determine the root loci in the broad neighborhood of the jω axis and the origin. The most important part of the root loci is on neither the real axis nor the asymptotes but the part in the broad neighborhood of the jω axis and the origin. The shape of the root loci in this important region in the s plane must be obtained with sufficient accuracy.

8. Determine closed-loop poles. A particular point on each root-locus branch will be a closed-loop pole if the value of K at that point satisfies the magnitude condition. Conversely, the magnitude condition enables us to determine the value of the gain K at any specific root location on the locus. (If necessary, the root loci may be graduated in terms of K. The root loci are continuous with K. )

The value of K corresponding to any point s on a root locus can be obtained using the magnitude condition, or

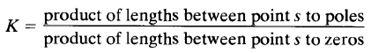
This value can be evaluated either graphically or analytically. If the gain K of the open-loop transfer function is given in the problem, then by applying the magnitude condition we can find the correct locations of the closed-loop poles for a given K on each branch of the root loci by a trial-and-error approach.