Integral And Derivative Factors In Bode Diagrams
The logarithmic magnitude of 1/jω in decibels is
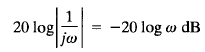
The phase angle of 1/jω is constant and equal to -90°. In Bode diagrams, frequency ratios are expressed in terms of octaves or decades. An octave is a frequency band from ω1 to 2ω1, where ω1 is any frequency value. A decade is a frequency band from ω1 to 10ω1, where again ω1 is any frequency. (On the logarithmic scale of semilog paper, any given frequency ratio can be represented by the same horizontal distance. For example, the horizontal distance from ω = 1 to ω = 10 is equal to that from ω = 3 to ω = 30.)
If the log magnitude -20 log ω dB is plotted against ω on a logarithmic scale, it is a straight line. To draw this straight line, we need to locate one point (0 dB, ω = 1) on it. Since

The phase angle of jω is constant and equal to 90°.The log-magnitude curve is a straight line with a slope of 20 dB/decade. Figures 1 (a) and (b) show frequency-response curves for 1/jω and jω, respectively. We can clearly see that the differences in the frequency responses of the factors 1/jω and jω lie in the signs of the slopes of the log magnitude curves and in the signs of the phase angles. Both log magnitudes become equal to 0 dB at ω = 1.
If the transfer function contains the factor (1/jω)n or (jω)n, the log magnitude becomes, respectively,
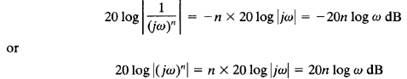
The slopes of the log-magnitude curves for the factors (1/jω)n and (jω)n are thus -20n dB/decade and 20n dB/decade, respectively. The phase angle of (1/jω)n is equal to - 90° X n over the entire frequency range, while that of (jω)n is equal to 90° X n over the entire frequency range. The magnitude curves will pass through the point (0 dB, ω = 1).