Introduction To Frequency-response Analysis
Introduction to Frequency-Response Analysis
The basic disadvantage of the frequency response method for analysis and design is the indirect link between the frequency and the time domain. Direct correlations between the frequency response and the corresponding transient response characteristics are somewhat tenuous, and in practice the frequency response characteristic is adjusted by using various design criteria that will normally result in a satisfactory transient response.
The Laplace transform pair is written as

where the complex variable s = σ jω. Similarly, the Fourier transform pair is written as
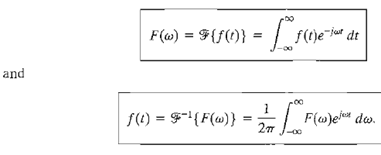
The Fourier transform exists for f(t) when
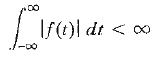
The Fourier and Laplace transforms are closely related. When the function f(t) is defined only for t ≥ 0, as is often the case, the lower limits on the integrals are the same. Then we note that the two equations differ only in the complex variable. Thus, if the Laplace transform of a function f1(t) is known to be F1(s), we can obtain the Fourier transform of this same time function by setting .s= jω in F1(s).
If we consider the frequency response of the closed-loop system, we might have an input r(t) that has a Fourier transform in the frequency domain as follows:
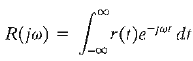
Then the output frequency response of a single-loop control system can be obtained by substituting s = jω in the closed-loop system relationship, Y(s) = T(s)R(s), so that we have
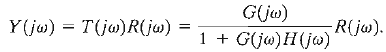
Using the inverse Fourier transform, the output transient response would be
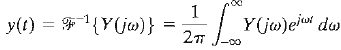
However, it is usually quite difficult to evaluate this inverse transform integral for all but the simplest systems, and a graphical integration may be used.