Mapping Theorem And Application

Mapping theorem

Let F(s) be a ratio of two polynomials in s. Let P be the number of poles and Z be the number of zeros of F(s) that lie inside some closed contour in the s plane, with multiplicity of poles and zeros accounted for. Let this contour be such that it does not pass through any poles or zeros of F(s). This closed contour in the s plane is then mapped into the F(s) plane as a closed curve. The total number N of clockwise encirclements of the origin of the F(s) plane, as a representative point s traces out the entire contour in the clockwise direction, is equal to Z - P. (Note that by this mapping theorem the numbers of zeros and of poles cannot be found, only their difference.)

We shall not present a formal proof of this theorem here but leave the proof to Problem A-8-10. Note that a positive number N indicates an excess of zeros over poles of the function F(s) and a negative N indicates an excess of poles over zeros. In control system applications, the number P can be readily determined for F(s) = 1 G(s)H(s) from the function G(s)H(s). Therefore, if N is determined from the plot of F(s), the number of zeros in the closed contour in the s plane can be determined readily. Note that the exact shapes of the s-plane contour and F(s) locus are immaterial so far as encirclements of the origin are concerned, since encirclements depend only on the enclosure of poles and/or zeros of F(s) by the s-plane contour.

 

Application of the mapping theorem to the stability analysis of closed-loop systems

 

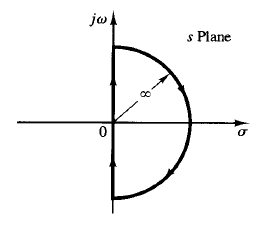
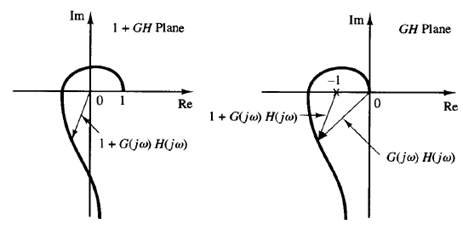
                 Fig: 1 Closed contour in the s plane                                                                       Fig: 2

For analyzing the stability of linear control systems, we let the closed contour in the s plane enclose the entire right-half s plane. The contour consists of the entire jω axis from ω = -∞ to ∞ and a semicircular path of infinite radius in the right half s plane. Such a contour is called the Nyquist path. (The direction of the path is clockwise.) The Nyquist path encloses the entire right-half s plane and encloses all the zeros and poles of 1 G(s)H(s) that have positive real parts.

[If there are no zeros of 1 G(s)H(s) in the right-half s plane, then there are no closed-loop poles there, and the system is stable.] It is necessary that the closed contour, or the Nyquist path, not pass through any zeros and poles of 1 G(s)H(s). If G(s)H(s) has a pole or poles at the origin of the s plane, mapping of the point s = 0 becomes indeterminate. In such cases, the origin is avoided by taking a detour around it. If the mapping theorem is applied to the special case in which F(s) is equal to 1 G(s)H(s), then we can make the following statement: If the closed contour in the s plane encloses the entire right-half s plane, as shown in Figure 1, then the number of right-half plane zeros of the function F(s) = 1 G(s)H(s) is equal to the number of poles of the function F(s) = 1 G(s)H(s) in the right-half s plane plus the number of clockwise encirclements of the origin of the 1 G(s)H(s) plane by the corresponding closed curve in this latter plane.

Because of the assumed condition that

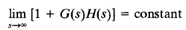
the function of 1 G(s)H(s) remains constant as s traverses the semicircle of infinite radius. Because of this, whether the locus of 1 G(s)H(s) encircles the origin of the 1 G(s)H(s) plane can be determined by considering only a part of the closed contour in the s plane, that is, the jω axis. Encirclements of the origin, if there are any, occur only while a representative point moves from - j∞ to j∞ along the jω axis, provided that no zeros or poles lie on the jω axis.

Note that the portion of the 1 G(s)H(s) contour from ω = -∞ to ω = ∞ is simply 1 G(jω)H(jω). Since 1 G(jω)H(jω) is the vector sum of the unit vector and the vector G(jω)H(jω), 1 G(jω)H(jω) is identical to the vector drawn from the -1 j0 point to the terminal point of the vector G(jω)H(jω), as shown in Figure 2. Encirclement of the origin by the graph of 1 G(jω)H(jω) is equivalent to encirclement of the -1 j0 point by just the G(jw)H(jw) locus. Thus, stability of a closed-loop system can be investigated by examining encirclements of the -1 j0 point by the locus of G(jω)H(jω). The number of clockwise encirclements of the -1 j0 point can be found by drawing a vector from the -1 j0 point to the G(jω)H(jω) locus, starting from ω = -∞, going through ω = 0, and ending at ω = ∞, and by counting the number of clockwise rotations of the vector.

Plotting G(jω)H(jω) for the Nyquist path is straightforward. The map of the negative jω axis is the mirror image about the real axis of the map of the positive jω axis. That is, the plot of G(jω)H(jω) and the plot of G( - jω)H( - jω) are symmetrical with each other about the real axis. The semicircle with infinite radius maps into either the origin of the GH plane or a point on the real axis of the GH plane.

G(s)H(s) has been assumed to be the ratio of two polynomials in s. Thus, the transport lag e^-Ts has been excluded.

The stability of a system with transport lag can be determined from the open-loop frequency-response curves by examining the number of encirclements of the -1 j0 point, just as in the case of a system whose open-loop transfer function is a ratio of two polynomials in s.