Nonlinear Systems

Nonlinear systems:

A system is nonlinear if the principle of superposition does not apply. Thus, for a nonlinear system the response to two inputs cannot be calculated by treating one input at a time and adding the results. Examples of nonlinear differential equations are

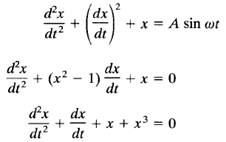
Although many physical relationships are often represented by linear equations, in most cases actual relationships are not quite linear. In fact, a careful study of physical systems reveals that even so-called "linear systems" are really linear only in limited operating ranges. In practice, many electromechanical systems, hydraulic systems, pneumatic systems, and so on, involve nonlinear relationships among the variables. For example, the output of a component may saturate for large input signals. There may be a dead space that affects small signals. (The dead space of a component is a small range of input variations to which the component is insensitive.) Square-law nonlinearity may occur in some components.

For instance, dampers used in physical systems may be linear for low-velocity operations but may become nonlinear at high velocities, and the damping force may become proportional to the square of the operating velocity. Examples of characteristic curves for these nonlinearities are shown in Figure. Note that some important control systems are nonlinear for signals of any size. For example, in on-off control systems, the control action is either on or off, and there is no linear relationship between the input and output of the controller.

Procedures for finding the solutions of problems involving such nonlinear systems, in general, are extremely complicated. Because of this mathematical difficulty attached to nonlinear systems, one often finds it necessary to introduce "equivalent" linear systems in place of nonlinear ones. Such equivalent linear systems are valid for only a limited range of operation. Once a nonlinear system is approximated by a linear mathematical model, a number of linear tools may be applied for analysis and design purposes.

 

 

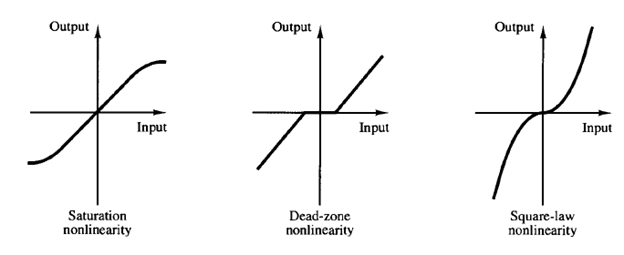
Fig: Characteristic curves for various nonlinearities.

 

Linearization of nonlinear systems:

 In control engineering a normal operation of the system may be around an equilibrium point, and the signals may be considered small signals around the equilibrium. (It should be pointed out that there are many exceptions to such a case.) However, if the system operates around an equilibrium point and if the signals involved are small signals, then it is possible to approximate the nonlinear system by a linear system. Such a linear system is equivalent to the nonlinear system considered within a limited operating range. Such a linearized model (linear, time-invariant model) is very important in control engineering.