Nyquist Stability Criterion Applied To Inverse Polar Plots

Nyquist stability criterion applied to inverse polar plots

In analyzing multiple-loop systems, the inverse transfer function may sometimes be used in order to permit graphical analysis; this avoids much of the numerical calculation. (The Nyquist stability criterion can be applied equally well to inverse polar plots. The mathematical derivation of the Nyquist stability criterion for inverse polar plots is the same as that for direct polar plots.)

The inverse polar plot of G(jω)H(jω) is a graph of 1/[G(jω)H(jω)] as a function of ω. For example, if G(jω)H(jω) is

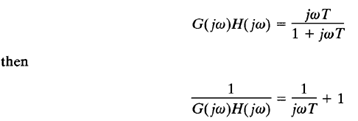
The inverse polar plot for ω ≥ 0 is the lower half of the vertical line starting at the point (1,0) on the real axis.

The Nyquist stability criterion applied to inverse plots may be stated as follows: For a closed-loop system to be stable, the encirclement, if any, of the -1 j0 point by the lI[G(s)H(s)] locus (as s moves along the Nyquist path) must be counterclockwise, and the number of such encirclements must be equal to the number of poles of 1/[G(s)H(s)] [that is, the zeros of G(s)H(s)] that lie in the right-half s plane. [The number of zeros of G(s)H(s) in the right-half s plane may be determined by use of the Routh stability criterion.]

If the open-loop transfer function G(s)H(s) has no zeros in the right-half s plane, then for a closed-loop system to be stable the number of encirclements of the -1 j0 point by the 1/[G(s)H(s)] locus must be zero.

Note that although the Nyquist stability criterion can be applied to inverse polar plots, if experimental frequency-response data are incorporated, counting the number of encirclements of the 1/[G(s)H(s)] locus may be difficult because the phase shift corresponding to the infinite semicircular path in the s plane is difficult to measure. For example, if the open-loop transfer function G(s)H(s) involves transport lag such that

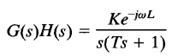
then the number of encirclements of the -1 j0 point by the 1/[G(s)H(s)] locus becomes infinite, and the Nyquist stability criterion cannot be applied to the inverse polar plot of such an open-loop transfer function.

In general, if experimental frequency-response data cannot be put into analytical form, both the G(jω)H(jω) and 1/[G(jω)H(jω)] loci must be plotted. In addition, the number of right-half plane zeros of G(s)H(s) must be determined. It is more difficult to determine the right-half plane zeros of G(s)H(s) (in other words, to determine whether a given component is minimum phase) than it is to determine the right-half plane poles of G(s)H(s) (in other words, to determine whether the component is stable).

Depending on whether the data are graphical or analytical and whether non minimum-phase components are included, an appropriate stability test must be used for multiple-loop systems. If the data are given in analytical form or if mathematical expressions for all the components are known, the application of the Nyquist stability criterion to inverse polar plots causes no difficulty, and multiple-loop systems may be analyzed and designed in the inverse GH plane