Orthogonality Of Root Loci And Constant-gain Loci

Orthogonality of root loci and constant-gain loci

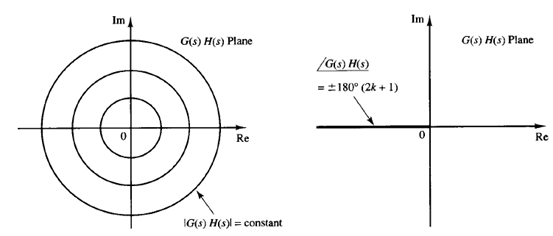
Fig: 1 Plots of constant gain and constant phase loci in the G(s)H(s) plane

Consider the system whose open-loop transfer function is G(s)H(s). In the G(s)H(s) plane, the loci of |G(s)H(s)| = constant are circles centered at the origin, and the loci corresponding to 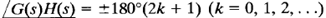lie on the negative real axis of the G(s)H(s) plane, as shown in Figure 1.

The root loci and constant-gain loci in the s plane are conformal mappings of the loci of 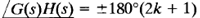and |G(s)H(s)| = constant in the G(s)H(s) plane.

Since the constant-phase and constant-gain loci in the G(s)H(s) plane are orthogonal, the root loci and constant-gain loci in the s plane are orthogonal. Figure 2(a) shows the root loci and constant-gain loci for the following system:

Notice that since the pole-zero configuration is symmetrical about the real axis the constant-gain loci are also symmetrical about the real axis.

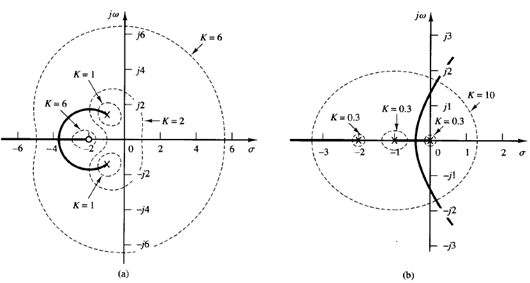
Fig: 2

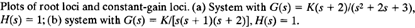
Figure 2(b) shows the root loci and constant-gain loci for the system:

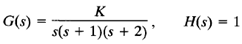
Notice that since the configuration of the poles in the s plane is symmetrical about the real axis and the line parallel to the imaginary axis passing through point (σ = -1,ω = 0), the constant-gain loci are symmetrical about the ω = 0 line (real axis) and the σ = -1 line.