Overdamped System
Overdamped system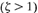 
:
In this case, the two poles of C(s)/R(s) are negative real and unequal. For a unit-step input, R(s) = 1/s and C(s) can be written
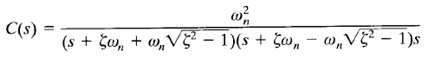
The inverse Laplace transform of Equation above can be written as
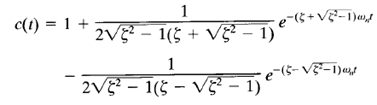
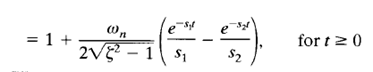
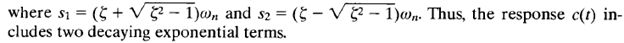
When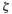 
is appreciably greater than unity, one of the two decaying exponentials decreases much faster than the other, so the faster decaying exponential term (which corresponds to a smaller time constant) may be neglected. That is, if –S2 is located very much closer to the jω axis than – S1 (which means |s2| << |S1|), then for an approximate solution we may neglect – S1.
This is permissible because the effect of – S1 on the response is much smaller than that of –S2, since the term involving s1 in the above equation of the inverse Laplace transform of C(s) decays much faster than the term involving s2. Once the faster decaying exponential term has disappeared, the response is similar to that of a first-order system, and C(s)/R(s) may be approximated by
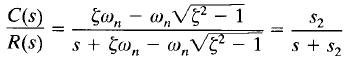
This approximate form is a direct consequence of the fact that the initial values and final values of both the original C(s)/R(s) and the approximate one agree with each other. With the approximate transfer function C(s)/R(s), the unit-step response can be obtained as
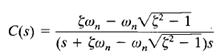
The time response c(t) is then
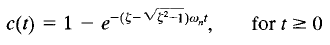
This gives an approximate unit-step response when one of the poles of C(s)/R(s) can be neglected.