Proportional-plus-derivative Control Of Second-order Systems
Proportional-plus-derivative control of second-order systems
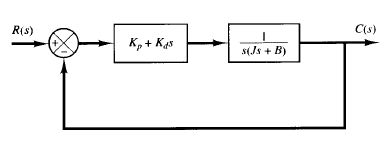
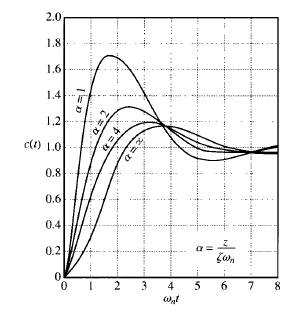
Fig: 1 Control system Fig: 2 Unit-step response curves of the second-order system
A compromise between acceptable transient-response behavior and acceptable steady-state behavior may be achieved by use of proportional-plus-derivative control action.
Consider the system shown in Figure 1. The closed-loop transfer function is
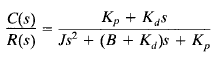
The steady-state error for a unit-ramp input is
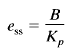
The characteristic equation is
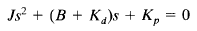
The effective damping coefficient of this system is thus B Kd rather than B. Since the damping ratio ζ of this system is
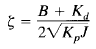
it is possible to make both the steady-state error ess for a ramp input and the maximum overshoot for a step input small by making B small, Kp large, and Kd large enough so that ζ is between 0.4 and 0.7.
In the following, we shall examine the unit-step response of the system shown in Figure 1. Let us define
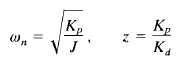
The closed-loop transfer function can then be written
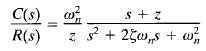
When a second-order system has a zero near the closed-loop poles, the transient response behavior becomes considerably different from that of a second-order system without a zero.
If the zero at s = - z is located close to the jω axis, the effect of the zero on the unit step response is quite significant. Typical step-response curves of this system with ζ = 0.5 and various values of z/(ζωn) are shown in Figure 2.