Quadratic Factors In Bode Diagram
Quadratic factors in Bode diagram
Control systems often possess quadratic factors of the form
If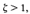 
this quadratic factor can be expressed as a product of two first-order factors with real poles. If 
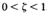, this quadratic factor is the product of two complex conjugate factors. Asymptotic approximations to the frequency-response curves are not accurate for a factor with low values of 
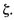This is because the magnitude and phase of the quadratic factor depend on both the corner frequency and the damping ratio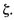
The asymptotic frequency-response curve may be obtained as follows:
Since
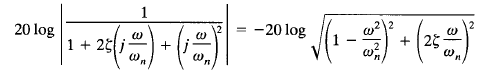
for low frequencies such that ω << ωn, the log magnitude becomes
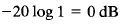
The low-frequency asymptote is thus a horizontal line at 0 dB. For high frequencies such that ω >> ωn, the log magnitude becomes
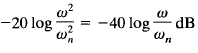
The equation for the high-frequency asymptote is a straight line having the slope -40 dB/decade since
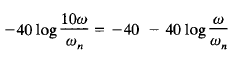
The high-frequency asymptote intersects the low-frequency one at ω = ωn since at this frequency
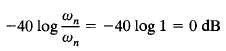
This frequency, ωn> is the corner frequency for the quadratic factor considered.
The two asymptotes just derived are independent of the value of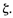 
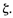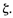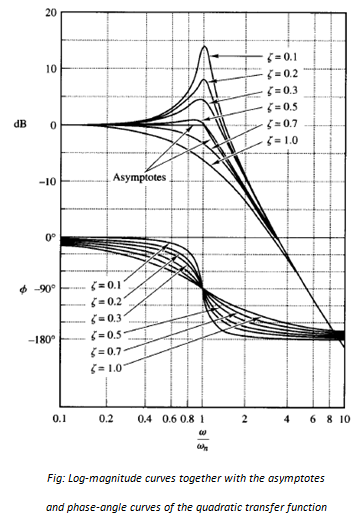
Near the frequency ω = ωn, a resonant peak occurs. The damping ratio determines the magnitude of this resonant peak. Errors obviously exist in the approximation by straight-line asymptotes. The magnitude of the error depends on the value of It is large for small values of 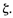Figure shows the exact log-magnitude curves together with the straight-line asymptotes and the exact phase-angle curves for the quadratic factor with several values of 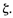If corrections are desired in the asymptotic curves, the necessary amounts of correction at a sufficient number of frequency points may be obtained from Figure.