Relative Stability Analysis By Conformal Mapping

Relative stability analysis by conformal mapping

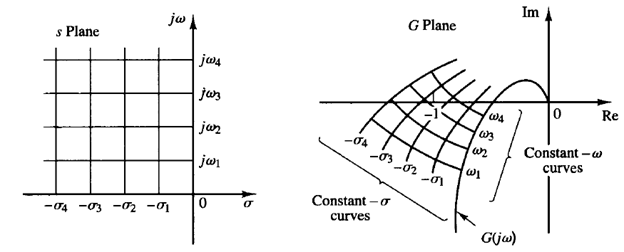
Fig: 1 conformal mapping of s-plane grids into the G(s) plane

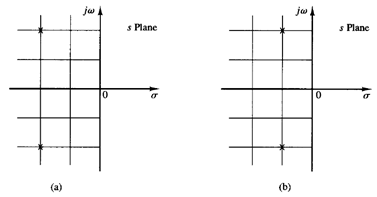
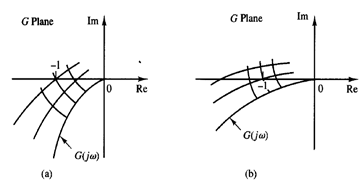
Fig 2: Two systems with two closed-loop poles                                Fig 3: Conformal mappings of s-plane grids for the systems shown in Fig 2 into the G(s) plane.

One of the important problems in analyzing a control system is to find all closed-loop poles or at least those closest to the jω axis (or the dominant pair of closed-loop poles). If the open-loop frequency-response characteristics of a system are known, it may be possible to estimate the closed-loop poles closest to the jω axis. It is noted that the Nyquist locus G(jω) need not be an analytically known function of w. The entire Nyquist locus may be experimentally obtained. The technique to be presented here is essentially graphical and is based on a conformal mapping of the s plane into the G(s) plane.

Consider the conformal mapping of constant-σ lines (lines s = σ jω, where a is constant and w varies) and constant-ω lines (lines s = σ jω, where ω is constant and σ varies) in the s plane. The σ = 0 line (the jω axis) in the s plane maps into the Nyquist plot in the G(s) plane. The constant-σ lines in the s plane map into curves that are similar to the Nyquist plot and are in a sense parallel to the Nyquist plot, as shown in Figure 1. The constant-w lines in the s plane map into curves, also shown in Figure 1.

Although the shapes of constant-σ and constant-ω loci in the G(s) plane and the closeness of approach of the G(jω) locus to the -1 j0 point depend on a particular G(s), the closeness of approach of the G(jω) locus to the -1 j0 point is an indication of the relative stability of a stable system. In general, we may expect that the closer the G(jω) locus is to the -1 j0 point, the larger the maximum overshoot is in the step transient response and the longer it takes to damp out.

Consider the two systems shown in Figure 2(a) and (b). (In Figure 2, the X's indicate closed-loop poles.) System (a) is obviously more stable than system (b) because the closed-loop poles of system (a) are located farther left than those of system (b). Figures 3(a) and (b) show the conformal mapping of s-plane grids into the G(s) plane. The closer the closed-loop poles are located to the jω axis, the closer the G(jω) locus is to the -1 j0 point.