Relative Stability Analysis Through Modified Nyquist Plots
Relative stability analysis through modified Nyquist plots
The Nyquist path for stability tests can be modified in order that we may investigate the relative stability of closed-loop systems. For the following second-order characteristic equation,
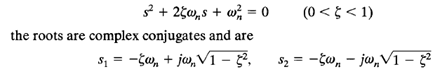
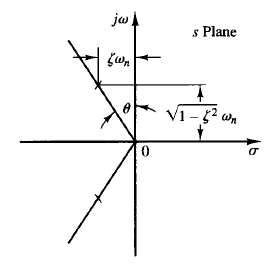
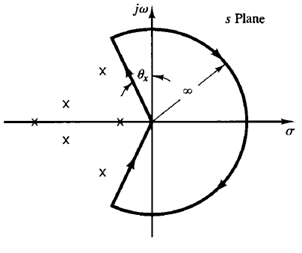
Fig: 1 Plot of complex-conjugate roots in the s plane Fig: 2 Modified Nyquist path
If these roots are plotted in the s plane, as shown in Figure 1, then we see that sinθ =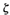 
, or the angle θ is indicative of the damping ratio 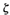. As θ becomes smaller, so does the value of .
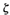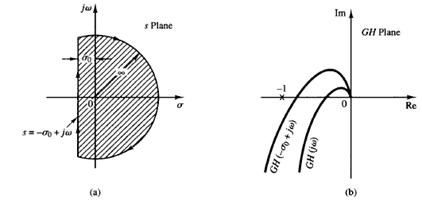
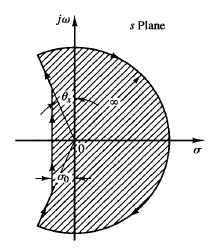
Fig: 3 Fig: 4
f we modify the Nyquist path and use radial lines with angle θx, instead of the jω axis, as shown in Figure 2, then it can be said, following the same reasoning as in the case of the Nyquist stability criterion, that if the G(s)H(s) locus corresponding to the modified s-plane contour does not encircle the -1 j0 point and none of the poles of G(s)H(s) lie within the closed s-plane contour then this contour does not enclose any zeros of 1 G(s)H(s). The characteristic equation, 1 G(s)H(s) = 0, then does not have any roots within the modified s-plane contour. If no closed-loop poles of a higher order system are enclosed by this contour, we can say that the damping ratio of each pair of complex-conjugate closed-loop poles of the system is greater than sin θx. Suppose that the s-plane contour consists of a line to the left of and parallel to the jω axis at a distance –σ0 (or the line s = -σ0 jω) and the semicircle of infinite radius enclosing the entire right-half s plane and that part of the left-half s plane between the lines s = -σ0 jω and s = jω, as shown in Figure 3(a). If the G(s)H(s) locus corresponding to this s-plane contour does not encircle the -1 j0 point and G(s)H(s) has no poles within the enclosed s-plane contour, then the characteristic equation does not have any zeros in the region enclosed by the modified s-plane contour. All roots of the characteristic equation lie to the left of the lines = -σ0 jω. An example of a G(-σ0 jω)H(-σ0 jω) locus, together with a G(jω)H(jω) locus, is shown in Figure 3(b).The magnitude 1/σ0 is indicative of the time constant of the dominant closed-loop poles. If all roots lie outside the s-plane contour, all time constants of the closed-loop transfer function are less than 1/σ0.1f the s-plane contour is chosen as shown in Figure 4, then the test of encirclements of the -1 j0 point reveals the existence or nonexistence of the roots of the characteristic equation of the closed-loop system within this s-plane contour. If the test reveals that no roots lie in the s-plane contour, then it is clear that all the closed loop poles have damping ratios greater than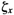 
and time constants less than 1/σ0.Thus, by taking an appropriate s-plane contour, we can investigate time constants and damping ratios of closed-loop poles from the open-loop transfer function.