Remarks On The Nyquist Stability Criterion
Nyquist stability criterion
The foregoing analysis, utilizing the encirclement of the -1 j0 point by the G(jω)H(jω) locus, is summarized in the following Nyquist stability criterion:
Nyquist stability criterion [for a special case when G(s)H(s) has neither poles nor zeros on the jω axis.]: In the system shown in Figure 1, if the open-loop transfer function G(s)H(s) has k poles in the right-half s plane and lims→∞G(s)H(s) = constant, then for stability the G(jω)H(jω) locus, as ω varies from -∞ to ∞, must encircle the -1 j0 point k times in the counterclockwise direction.
Remarks on the Nyquist stability criterion
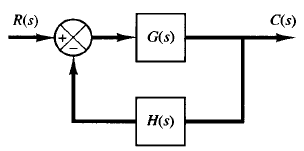
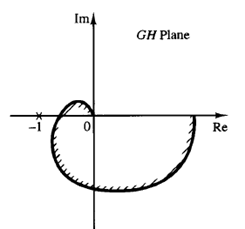
Fig: 1 Closed loop system Fig: 2 Region enclosed by a Nyquist plot.
1. This criterion can be expressed as Z=N P
Where Z = number of zeros of 1 G(s)H(s) in the right-half s plane
N = number of clockwise encirclements of the -1 j0 point
P = number of poles of G(s)H(s) in the right-half s plane
If P is not zero, for a stable control system, we must have Z = 0, or N = - P, which means that we must have P counterclockwise encirclements of the -1 j0 point. If G(s)H(s) does not have any poles in the right-half s plane, then Z = N. Thus, for stability there must be no encirclement of the -1 j0 point by the G(jω)H(jω) locus.
In this case it is not necessary to consider the locus for the entire jω axis, only for the positive-frequency portion. The stability of such a system can be determined by seeing if the -1 j0 point is enclosed by the Nyquist plot of G(jω)H(jω).The region enclosed by the Nyquist plot is shown in Figure 2. For stability, the -1 j0 point must lie outside the shaded region.
2. We must be careful when testing the stability of multiple-loop systems since they may include poles in the right-half s plane. (Note that although an inner loop may be unstable the entire closed-loop system can be made stable by proper design.) Simple inspection of encirclements of the -1 j0 point by the G(jω )H(jω) locus is not sufficient to detect instability in multiple-loop systems. In such cases, however, whether any pole of 1 G(s)H(s) is in the right-half s plane can be determined easily by applying the Routh stability criterion to the denominator of G(s)H(s).
If transcendental functions, such as transport lag e-Ts, are included in G(s)H(s), they must be approximated by a series expansion before the Routh stability criterion can be applied. One form of a series expansion of e-Ts is given as:
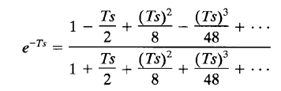
As a first approximation, we may take only the first two terms in the numerator and denominator, respectively, or
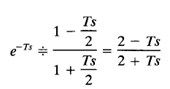
This gives a good approximation to transport lag for the frequency range 0 ≤ ω ≤ (O.5/T).
[Note that the magnitude of (2 - jωT)(2 jωT) is always unity, and the phase lag of (2 - jωT)/(2 jωT) closely approximates that of transport lag within the stated frequency range.]
3. If the locus of G(jω )H(jω) passes through the -1 j0 point, then zeros of the characteristic equation, or closed-loop poles, are located on the jω axis. This is not desirable for practical control systems. For a well-designed closed-loop system, none of the roots of the characteristic equation should lie on the jω axis.