Root-contour Plots - Effects Of Parameter Variations On Closed-loop Poles
Root-contour plots
Effects of parameter variations on closed-loop poles
In many design problems, the effects on the closed-loop poles of the variations of parameters other than the gain K need to be investigated. Such effects can be easily investigated by the root-locus method. When two (or more) parameters are varied, the corresponding root loci are called root contours.
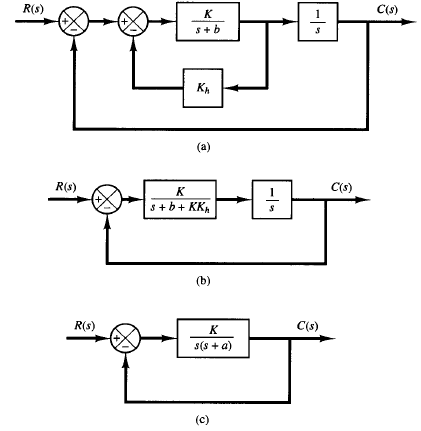
Fig: 1 (a) Servo system with tachometer feedback; (b), (c) simplified block diagrams (a = b KKh)
We shall use an example to illustrate the construction of the root contours when two parameters are varied, respectively, from zero to infinity. Consider a servo system having tachometer feedback as shown in Figure 1(a). By eliminating the minor loop, the block diagram can be simplified [Figure 1(b)].
By defining
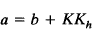
this block diagram can be modified to that shown in Figure 1(c). This system involves two variables, parameter a and gain K. In what follows we shall investigate the effect of varying the parameter a as well as the gain K. The closed-loop transfer function of this system becomes
