Rouths Stability Criterion
Routh's stability criterion
Since most linear closed-loop systems have closed-loop transfer functions of the form
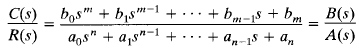
where the a's and b's are constants and m ≤ n, we must first factor the polynomial A(s) in order to find the closed-loop poles. A simple criterion, known as Routh's stability criterion, enables us to determine the number of closed-loop poles that lie in the right-half s plane without having to factor the polynomial.
Routh's stability criterion tells us whether or not there are unstable roots in a polynomial equation without actually solving for them. This stability criterion applies to polynomials with only a finite number of terms. When the criterion is applied to a control system, information about absolute stability can be obtained directly from the coefficients of the characteristic equation.
The procedure in Routh's stability criterion is as follows:
1. Write the polynomial in s in the following form:
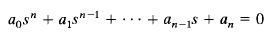
where the coefficients are real quantities. We assume that an ≠ 0; that is, any zero root has been removed.
2. If any of the coefficients are zero or negative in the presence of at least one positive coefficient, there is a root or roots that are imaginary or that have positive real parts. Therefore, in such a case, the system is not stable. If we are interested in only the absolute stability, there is no need to follow the procedure further. Note that all the coefficients must be positive.
This is a necessary condition, as may be seen from the following argument: A polynomial in s having real coefficients can always be factored into linear and quadratic factors, such as (s a) and (S2 bs c), where a, b, and c are real. The linear factors yield real roots and the quadratic factors yield complex roots of the polynomial.
The factor (S2 bs c) yields roots having negative real parts only if band c are both positive. For all roots to have negative real parts, the constants a, b, c, and so on, in all factors must be positive. The product of any number of linear and quadratic factors containing only positive coefficients always yields a polynomial with positive coefficients. It is important to note that the condition that all the coefficients be positive is not sufficient to assure stability.
The necessary but not sufficient condition for stability is that the coefficients of Equation in (1) all be present and all have a positive sign. (If all a's are negative, they can be made positive by multiplying both sides of the equation by -1.)