Second-order Systems Settling Time
Second-order systems settling Time
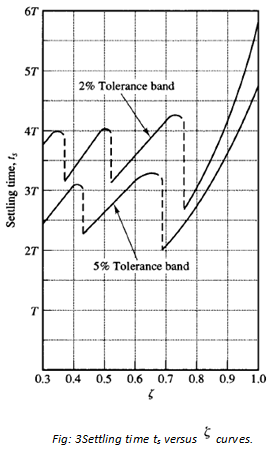
The results are shown in Figure 3. For 0 <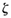 
< 0.9, if the 2% criterion is used ts is approximately four times the time constant of the system. If the 5% criterion is used, then ts is approximately three times the time constant. Note that the settling time reaches a minimum value around l; = 0.76 (for the 2% criterion) or 
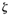= 0.68 (for the 5% criterion) and then increases almost linearly for large values of 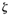. The discontinuities in the curves of Figure 3 arise because an infinitesimal change in the value of 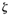can cause a finite change in the settling time. For convenience in comparing the responses of systems, we commonly define the settling time ts to be
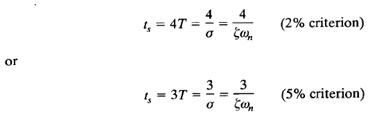
Note that the settling time is inversely proportional to the product of the damping ratio and the undamped natural frequency of the system. Since the value of 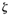is usually determined from the requirement of permissible maximum overshoot, the settling time is determined primarily by the undamped natural frequency ωn. This means that the duration of the transient period may be varied, without changing the maximum overshoot, by adjusting the undamped natural frequency ωn.
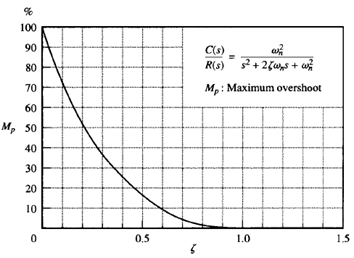
Fig: 4 Mp versus 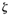curve.
From the preceding analysis, it is evident that for rapid response ωn must be large. To limit the maximum overshoot Mp and to make the settling time small, the damping ratio 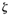should not be too small. The relationship between the maximum percent overshoot Mp and the damping ratio 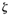is presented in Figure 4. Note that if the damping ratio is between 0.4 and 0.8 then the maximum percent overshoot for step response is between 25% and 2.5%.