Stability Analysis In The Complex Plane
Stability analysis in the complex plane
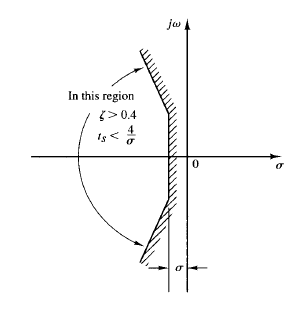
Fig: 1 Region in the complex plane
The stability of a linear closed-loop system can be determined from the location of the closed-loop poles in the s plane. If any of these poles lie in the right-half s plane, then with increasing time they give rise to the dominant mode, and the transient response increases monotonically or oscillates with increasing amplitude.
This represents an unstable system. For such a system, as soon as the power is turned on, the output may increase with time. If no saturation takes place in the system and no mechanical stop is provided, then the system may eventually be subjected to damage and fail since the response of a real physical system cannot increase indefinitely. Therefore, closed-loop poles in the right-half s plane are not permissible in the usual linear control system. If all closed-loop poles lie to the left of the jω axis, any transient response eventually reaches equilibrium. This represents a stable system.
Whether a linear system is stable or unstable is a property of the system itself and does not depend on the input or driving function of the system. The poles of the input, or driving function, do not affect the property of stability of the system, but they contribute only to steady-state response terms in the solution. Thus, the problem of absolute stability can be solved readily by choosing no closed-loop poles in the right-half s plane, including the jω axis. (Mathematically, closed-loop poles on the jw axis will yield oscillations, the amplitude of which is neither decaying nor growing with time.
In practical cases, where noise is present, however, the amplitude of oscillations may increase at a rate determined by the noise power level. Therefore, a control system should not have closed-loop poles on the jω axis.)
Note that the mere fact that all closed-loop poles lie in the left-half s plane does not guarantee satisfactory transient-response characteristics. If dominant complex conjugate closed-loop poles lie close to the jω axis, the transient response may exhibit excessive oscillations or may be very slow. Therefore, to guarantee fast, yet well damped, transient-response characteristics, it is necessary that the closed-loop poles of the system lie in a particular region in the complex plane, such as the region bounded by the shaded area in Figure 1.
Since the relative stability and transient performance of a closed-loop control system are directly related to the closed-loop pole-zero configuration in the s plane, it is frequently necessary to adjust one or more system parameters in order to obtain suitable configurations.