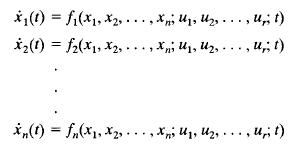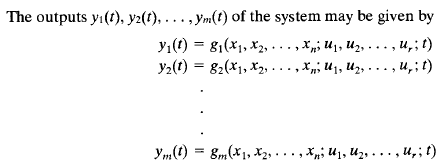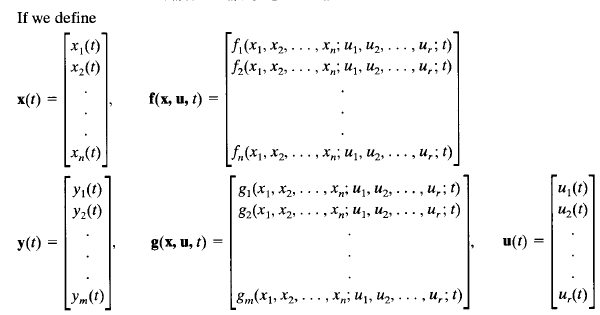State-space Equations
State-space equations
In state-space analysis we are concerned with three types of variables that are involved in the modeling of dynamic systems: input variables, output variables, and state variables. The state space representation for a given system is not unique, except that the number of state variables is the same for any of the different state-space representations of the same system.
The dynamic system must involve elements that memorize the values of the input for t ≥ t1. Since integrators in a continuous-time control system serve as memory devices, the outputs of such integrators can be considered as the variables that define the internal state of the dynamic system. Thus the outputs of integrators serve as state variables. The number of state variables to completely define the dynamics of the system is equal to the number of integrators involved in the system.
Assume that a multiple-input-multiple-output system involves n integrators. Assume also that there are r inputs u1, u2(t), ... ,ur(t) and m outputs Y1(t), Y2(t), ... , Ym(t). Define n outputs of the integrators as state variables: x1(t), x2(t), ... ,xn(t). Then the system may be described by