Step Response Of Second-order Systems
Step response of second-order systems
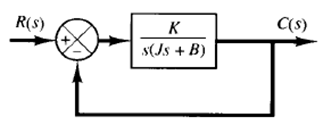
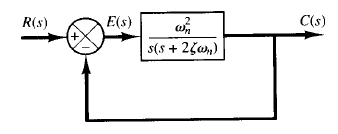
Fig: 1 Fig: 2 Second-order system.
The closed-loop transfer function of the system shown in Figure 1 is
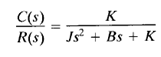
Which can be written as
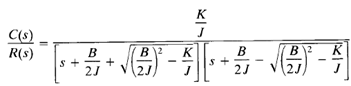
The closed-loop poles are complex if B2 - 4JK < 0, and they are real if B2 - 4JK ≥ 0. In transient-response analysis, it is convenient to write
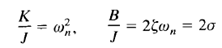
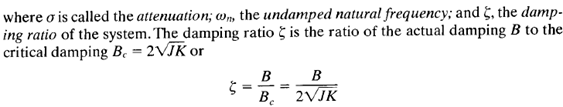
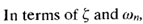the system shown in Figure 1(c) can be modified to that shown in Figure 2, and the closed-loop transfer function C(s)/R(s) can be written as
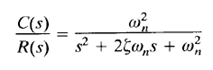
The dynamic behavior of the second-order system can then be described in terms of two parameters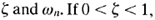 
the closed-loop poles are complex conjugates and lie in the left-half s plane. The system is then called underdamped, and the transient response is oscillatory. If 
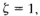the system is called critically damped. Overdamped systems correspond to
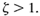The transient response of critically damped and overdamped systems do not oscillate. 
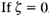, the transient response does not die out.