The Relative Stability Of Feedback Control Systems
The relative stability of feedback control systems
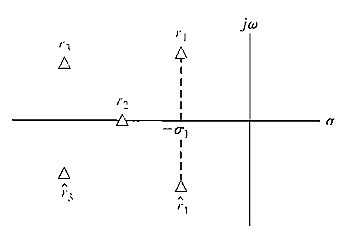
Fig: Root locations in the s-plane.
The verification of stability using the Routh-Hurwitz criterion provides only a partial answer to the question of stability. The Routh-Hurwitz criterion ascertains the absolute stability of a system by determining whether any of the roots of the characteristic equation lie in the right half of the s-plane.
However, if the system satisfies the Routh-Hurwitz criterion and is absolutely stable, it is desirable to determine the relative stability; that is, it is necessary to investigate the relative damping of each root of the characteristic equation. The relative stability of a system can be defined as the property that is measured by the relative real part of each root or pair of roots.
Thus, root r2 is relatively more stable than the roots r1, r^1 as shown in Figure 1. The relative stability of a system can also be defined in terms of the relative damping coefficients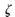 
of each complex root pair and, therefore, in terms of the speed of response and overshoot instead of settling time.
Hence, the investigation of the relative stability of each root is clearly necessary because, the location of the closed-loop poles in the s-plane determines the performance of the system. Thus, it is imperative that we reexamine the characteristic polynomial q(s) and consider several methods for the determination of relative stability.
Because the relative stability of a system is dictated by the location of the roots of the characteristic equation, a first approach using an s-plane formulation is to extend the Routh-Hurwitz criterion to ascertain relative stability.
This can be simply accomplished by utilizing a change of variable, which shifts the s-plane axis in order to utilize the Routh-Hurwitz criterion. Examining Figure 1, we notice that a shift of the vertical axis in the s-plane to — σ1 will result in the roots r1, r^1, appearing on the shifted axis. The correct magnitude to shift the vertical axis must be obtained on a trial-and-error basis. Then, without solving the fifth-order polynomial q(s), we may determine the real part of the dominant roots r1, r^1.