The Resonant Frequency & The Resonant Peak Value
The resonant frequency & the resonant peak value
The magnitude of
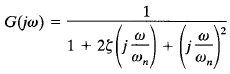
is
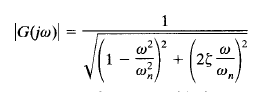
If |G(jω)| has a peak value at some frequency, this frequency is called the resonant frequency. Since the numerator of |G(jω)| is constant, a peak value of |G(jω)| will occur when
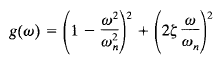
is a minimum. Since the above equation can be written as
the minimum value of g(ω) occurs at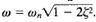 
Thus the resonant frequency ωr is
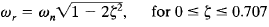
As the damping ratio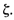 
approaches zero, the resonant frequency approaches wn. For o< 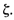≤0.707, the resonant frequency ωr is less than the damped natural frequency 
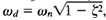which is exhibited in the transient response.
From the above equation it can be seen that for 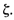> 0.707 there is no resonant peak. The magnitude |G(jω)|decreases monotonically with increasing frequency ω. (The magnitude is less than 0 dB for all values of ω > 0. Recall that, for 0.7 < 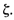< 1, the step response is oscillatory, but the oscillations are well damped and are hardly perceptible.). The magnitude of the resonant peak Mr can be found by substituting the above equation into the equation of the magnitude of G(jω). For 0 ≤ 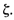≤ 0.707,
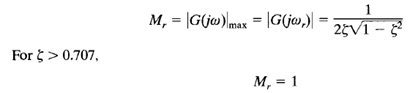
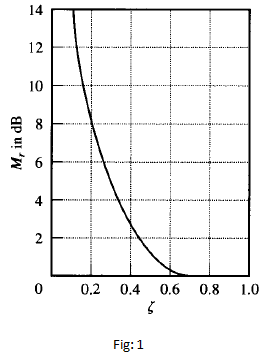
As 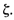approaches zero, Mr approaches infinity. This means that if the undamped system is excited at its natural frequency the magnitude of G(jω)becomes infinity. The relationship between Mr and 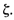is shown in Figure 1.
The phase angle of G(jω) at the frequency where the resonant peak occurs can be obtained by substituting the resonant frequency equation into Equation
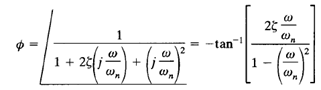
Thus, at the resonant frequency ωr,
