The Stability Of State Variable Systems

The stability of state variable systems:

The stability of a system modeled by a state variable flow graph model can be readily ascertained. The stability of a system with an input-output transfer function T(s) can be determined by examining the denominator polynomial of T(s). Therefore, if the transfer function is written as

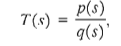
where p(s) and q(s) are polynomials in s, then the stability of the system is represented by the roots of q(s). The polynomial q(s), when set equal to zero, is called the characteristic equation.

The roots of the characteristic equation must lie in the lefthand s-plane for the system to exhibit a stable time response. Therefore, to ascertain the stability of a system represented by a transfer function, we investigate the characteristic equation and utilize the Routh-Hurwitz criterion.

If the system we are investigating is represented by a signal-flow graph state model, we obtain the characteristic equation by evaluating the flow graph determinant. If the system is represented by a block diagram model we obtain the characteristic equation using the block diagram reduction methods.

EXMAPLE - Stability of a system

Let us consider a transfer function T(s),

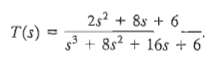
The characteristic polynomial for this system is

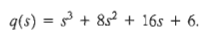
This characteristic polynomial is also readily obtained from either the flow graph model or block diagram model.

Using the Routh-Hurwitz criterion, we find that the system is stable and that all the roots of q(s) lie in the left-hand s-plane.

We often determine the flow graph or block diagram model directly from a set of state differential equations. We can use the flow graph directly to determine the
stability of the system by obtaining the characteristic equation from the flow graph determinant Δ(s). Similarly, we can use block diagram reduction to define the characteristic equation.