The Transfer Function Of Linear Systems
THE TRANSFER FUNCTION OF LINEAR SYSTEMS
The transfer function of a linear system is defined as the ratio of the Laplace transform of the output variable to the Laplace transform of the input variable, with all initial conditions assumed to be zero. The transfer function of a system (or element) represents the relationship describing the dynamics of the system under consideration.
A transfer function may be defined only for a linear, stationary (constant parameter) system. A non-stationary system, often called a time-varying system, has one or more time-varying parameters, and the Laplace transformation may not be utilized. Furthermore, a transfer function is an input-output description of the behavior of a system.
Thus, the transfer function description does not include any information concerning the internal structure of the system and its behavior. The transfer function of the spring-mass-damper system is obtained from the original equation
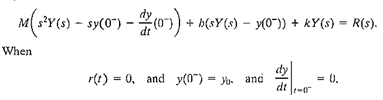
rewritten with zero initial conditions as follows:
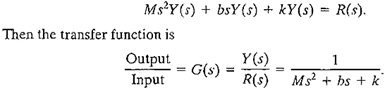
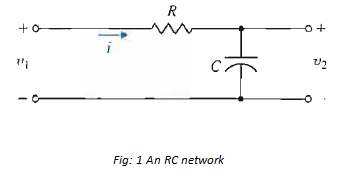
The transfer function of the RC network shown in Figure 1 is obtained by writing the Kirchhoff voltage equation, yielding
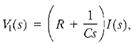
expressed in terms of transform variables. We shall frequently refer to variables and their transforms interchangeably. The transform variable will be distinguishable by the use of an uppercase letter or the argument (s).
The output voltage is
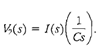
Therefore, solving the above equations, we have,
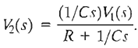
Then the transfer function is obtained as the ratio V2(s)/V1(s), which is
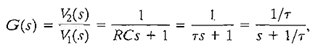
where τ = RC, the time constant of the network. The single pole of G(s) is s = — 1/τ.