Transfer Functions Of Cascaded Elements
Transfer functions of cascaded elements:
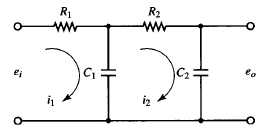
Fig: 1
Many feedback systems have components that load each other. Consider the system shown in Figure 3-19. Assume that e1 is the input and eo is the output. In this system the second stage of the circuit (R2C2 portion) produces a loading effect on the first stage (R1C1 portion). The equations for this system are
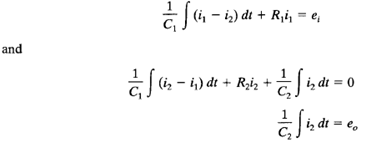
Taking the Laplace transforms of Equations assuming zero initial conditions, we obtain
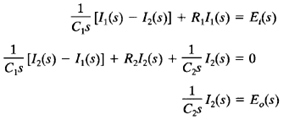
Eliminating I1(s) from the above equations and writing Ei(s) in terms of l2(s), we find the transfer function between E0(s) and Ei(s) to be
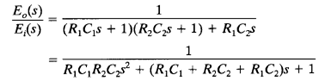
The term R1C2S in the denominator of the transfer function represents the interaction of two simple RC circuits. Since (R1C1 R2C2 R1C2)2 > 4R1C1R2C2, the two roots of the denominator of Equation above are real.
The present analysis shows that, if two RC circuits are connected in cascade so that the output from the first circuit is the input to the second, the overall transfer function is not the product of 1/(R1C1S 1) and 1/(R2C2s 1). The reason for this is that, when we derive the transfer function for an isolated circuit, we implicitly assume that the output is unloaded.
In other words, the load impedance is assumed to be infinite, which means that no power is being withdrawn at the output. When the second circuit is connected to the output of the first, however, a certain amount of power is withdrawn, and thus the assumption of no loading is violated. Therefore, if the transfer function of this system is obtained under the assumption of no loading, then it is not valid. The degree of the loading effect determines the amount of modification of the transfer function.